RAPIS024

/*    RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA

Egzamin - Inżynieria Produkcji - 2.02.2005

1.    (5 pkt) Zmienna losowa X ma rozkład prawdopodobieństwa postaci: P(X = —2) = 0.5, P{X = -1) = 0.2, P(X = 1) = 0.3.

Oblicz a) dystrybuantę zmiennej losowej X, b) wariancję X, c) kwanty) rzędu 0.8 zmiennej losowej X, d) medianę X, e) modę.

2.    (5 pkt) Wylosowano 400 studentów pewnego wydziału i poddano ich egzaminowi. Otrzymano średnią Ocenę z próby x = 3.1 oraz wariancje z próby A² = 0.25. Przy współczynniku ufności 1 — a — 0.98 znaleźć przedział ufności dla nieznanej wartości oczekiwanej (średniej) oceny z tego egzaminu dla wszystkich studentów tego wydziału.

V

3.    (5 pkt) Wykonano 26 pomiarów pewnym przyrządem i otrzymano odchylenie standardowe z próby s = 0.6. Na poziomic istotności a = 0.1 zweryfikować hipotezę, żc wariancja pomiarów

' tym przyrządem jest mniejsza niż 0.4.

4.    (za każdą prawidłową odpowiedź: + 1 pkt, za każdą złą odpowiedzą -1 pkt, za brak odpowiedzi: O pkt) Czy poniższe zdanie jest prawdziwe:

| (aj Prawdopodobieństwo jest funkcją nieujemną.

'f- (€) Jeśli P(A) = 0.2 oraz P(B) = 0.5 oraz A C D, to P(D \ A) 0.3.-e"

T (c) Przy jednokrotnym rzucie kostką sześcienną zdarzenia:^- wy^rpadla parzysta liczba oczek i B- wypadła nieparzysta liczba oczek są niezależne. \ KI i

t\\ (d) Funkcja F(x) = jf dla £ € R jest dystrybuantą pewnej zmiennej losowej. f-J^: = f\J (e) Dystrybuanta zmiennej losowej X może przyjąć wartość 2.    fJ

^ —fyr (f) Funkcja gęstości prawdopodobieństwa nie może osiągać wartości większych niż 1. tsf r® Mediana je^t kwantyjem rzęrłu    ^    J- -

-7 (fi) Jeżeli P(X^d) to E(X) = 0.    ™    '

^\(i) Wariancja jest kwadratem odchylenia standardowego. .W _    ,

' ^C \ N 0) Wariancja zmiennej losowej o rozkładzie A^r(2,4) wynosi 4. vJ \    ⁰    ^

i ^ ^|,^x^r(k) W rozkładzie Bernoulliego B( 100,0.1) odchylenie standardowe wynosi 3.    f '"P)

■' ^    (0' zmienna losowa X ma rozkład AT(1,1), to zmienna losowa X — 1 ma rozkład A’(0,1). ^7\K

• ’^#,^’(rn) Zmienna losowa o rozkładzie jednostajnym ha" przedziale (0,1) ma wariancję rówuą 1. Hit \ (n)j Wykład z RAPiS dla Inżynierii Produkcji w tym semestrze odbywał sję wc wtorki.

*ł-(o) Średnia z próby jest estymatorem wartości oczekiwanej.    ^

Zaliczenie egzaminu następuje przy otrzymaniu co najmniej 15 punktów w tym co najmniej +5 punktów za zadanię,4_.(testowe).

&

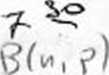
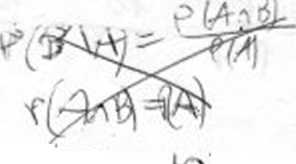
*$$) 71

b

£X- “f

't)

. ' W-f