skan0056

Termodynamika chemiczna 59

Łatwo sprawdzić, że obliczając pracę w procesie nieodwracalnym ze wzoru 13.25), przy wykorzystaniu wartości parametrów z powyższej tabeli, otrzymamy taki sam wynik (-450 J). ■

Przykład 3.5. W izoentalpowym procesie Joule’a-Thomsona gaz rzeczywisty ulega adiabatycznej ekspansji, w której

^- /*//»

gdzie p_H jest tzw. współczynnikiem Joule’a-Thomsona. Dla powietrza w 0°C, u_H = 0,249 K • atm^-1 dla p_x = 20 atm oraz p_H = 0,266 K ■ atirf¹ dla p₂ = 1 atm. Obliczyć, o ile obniży się temperatura powietrza w adiabatycznym procesie ekspansji od 20 atm do 1 atm.

Rozwiązanie. Z definicji współczynnika Joule’a-Thomsona wynika, że

Pi

AT= J p_Hdp.

Pi

Na podstawie powyższych danych, zależność ciśnieniowa współczynnika Joule^?a-Thoinsona w tym zakresie jest linią prostą o równaniu

p_H= a + bp = 0,26689 - 8,9474 • 10~⁴ p, toteż, po scałkowaniu, otrzymamy

AT=a(p₂-p\) + \ipl-p\) =

8 9474

= 0,26689 • (-19)-    2    ' 10-⁴-(1 -400) = -4,89 K.

W gazach rzeczywistych, poniżej temperatury inwersji^, gdziep_H> 0, adiabatyczne rozprężanie gazu związane jest z wykonaniem pracy przeciwko siłom przyciągania cząsteczek. Dla gazu idealnego, oczywiście, p_H= 0, gdyż

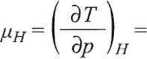
T (d V/d T)_p - V

Standardowa entalpia tworzenia AH₂₉% związku chemicznego jest zmianą entalpii fikcyjnej reakcji tworzenia 1 mola tego związku z pierwiastków w ich fazach stabilnych w warunkach standardowych (298,15 K, 1 bar). W starszych

⁽ⁿ Te temperatur)’ są zwykle dość wysokie, np. dla powietrza T_inw = 760 K. Wyjątkiem jest wodór (7j_nw ⁼ 204,7 K) i hel (T_inw = 40 K).