skan0068

Termodynamika chemiczna 71

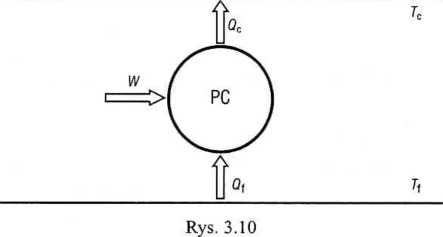
ze sprawność urządzenia jest zawsze wielkością dodatnią, a zatem, uwzględniane dodatkowo wyrażenie (3.40), otrzymujemy

Qc ₌ T_c

^r] W T_c - Tf '

Przy zmieniającej się cały czas temperaturze zbiornika poprawniej jest ją zdefiniować jako wielkość chwilową, zależną od temperatury'

(gęk _ T ^nr W_d T-Tf •

Tak więc:

(<2c)d = ~mcdT=-W_cl ^T => W_eX = ^{T Tf} mcdT.

1 — 1 f    1

-o scałkowaniu w granicach od T_p = 288 K, do T_k = 353 K otrzymamy wartość

pracy

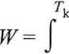
m c

T-T_f

dT - m c

(r_k-r_p)-7fin

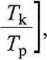
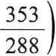
31 • 10³ kJ (8,6 kWh).

W= 4,184- 10³ 65 - 283 - In

W podobny sposób możemy obliczyć ilość ciepła dostarczonego do zbiorni-•_a z wodą

h

2c = -J    mcdT = —mc

_atem Q_c = -1000 ■ 4,184 • 65 = -272 ■ 10³ kJ, a z równania bilansu (I zasada) W+ ~ Q_c ⁺ Qf ⁼ 0 możemy obliczyć ciepło pobrane z jeziora i równe Q_f = 241 • 10³ kJ.

b) podgrzewając wodę energią grzałki elektrycznej równą obliczonej pracy W, “zożna osiągnąć temperaturę końcową