str076 (5)

76 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Podstawiając wzory (4) i (5) do wzoru (3), mamy

+ 00

I

e^,xdx

(x² + l)(x² + 9)

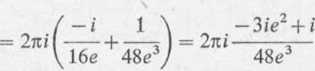
tc(3c²-1) 24e³    ’

+ co

f

— oc

— 00

(6)

e^ixdx

(x² + l)(x²+9)

7t(3e²-l) 24?    '

Przekształcając lewą stronę wzoru (6) w celu wydzielenia części rzeczywistej i urojonej, mamy

* w

I

e^,xdx

= 1

cos x +1 sin x

(x +l)(x +9) J (x + l)(x +9)

dx =

— 00 + oo

-J

cos x dx

(x +l)(x +9)

+ i

sin x dx

(x² + 1)(x² + 9)’

Wobec tego

(7)

+ 00

I

cos x dx

"ł" /

-t- a

I

sinxrfx    7t(3e² — 1)

(x + l)(x +9) J (x +l)(x +9)    24e

otrzymujemy wtedy

(U)

Widać natychmiast, że tylko p Biorąc powyższe pod uwagę i st otrzymujemy w rozważanym p

+ <

(12)    J

Zgodnie ze wzorem (10.2') zi z, = (1 + 3/), mamy

(13)    res.,/(z) = res*

₌ (1 + 2

Podstawiając (13) do (12), ma

+ OO

r xe^ixdx x² — 2x+lC

Porównując części rzeczywiste i urojone po obu stronach wzoru (7), mamy

+ 00

(8)

cosx

J (x² + l)(

dx

jt(3e — 1)

l)(x +9)    24e

— 00

+ OO

(9)

J (*² +

sin x dx

+ l)(x +9)

= 0.

Wynik określony wzorem (9) jest banalny, można go bowiem otrzymać wykorzystując fakt, że funkcja podcałkowa w (9) jest nieparzysta, b) Bierzemy pod uwagę funkcję

czyli	+ 00
(14)	l — 00

xe ^Xdx

-2x + l

Zauważmy teraz, że lewą sti

r

+ oo

(10)

/(-) =

ze'

xe^ixdx

z — 2z+10’

(15)

2x + l

której część rzeczywista dla rzeczywistych wartości z — x pokrywa się z funkcją podcałkową. Zauważmy teraz, że funkcja określona wzorem (10) spełnia założenia lematu Jordana. Stwierdzamy następnie, że funkcja ta ma dwa bieguny, z których każdy jest jednokrotny. Bieguny te są miejscami zerowymi funkcji (z² —2z+10). W celu znalezienia tych miejsc zerowych rozwiązujemy równanie

Wobec wzorów (14) i (15) i

(16)

z²—2z + 10 = 0,

+ 00

[* xcos xdx . [

J ?^+Tó⁺‘ J