str110 (5)

110 . ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

110 . ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

(2)

Rozwiązując układ (1), otrzymujemy

x_l = —24, x₂ = 0 (lub *! = 0, x₂ = —24).

Jeden z tych punktów winien przejść w punkt w = 0, drugi zaś w punkt w = co. Załóżmy najpierw, że punkt z_t = x_t = — 24 przechodzi w punkt w = 0, a punkt z₂ = x₂ = 0 w punkt w — oo. Wówczas szukana funkcja homograficzna będzie postaci

, z+24 w = k-

gdzie współczynnik k jest na razie dowolny.

Podstawiając równość (3) ficzna, realizująca żądane od

(4)

gdzie a to dowolna liczba r;

Przyjmując we wzorze (4) promień okręgu wewnętrznej z = 24 otrzymujemy ze wzo

Rys. 1.35

Zatem promień okręgu nosi i.

Uwaga. Rozpatrując pn otrzymujemy w sposób zupę

(5)

gdzie a jest dowolną liczbą

Zadanie 11.14. Znaleźć p przy odwzorowaniu w = z². Rozwiązanie. Aby zna

w = k

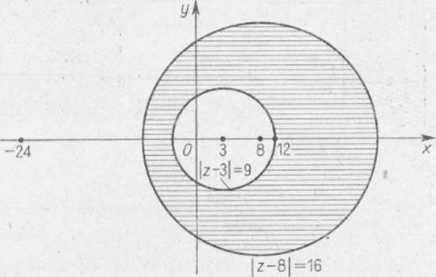
Ponieważ punkt z = 0, wewnętrzny względem obu danych okręgów, przechodzi w punkt w = oo, który jest punktem zewnętrznym względem obrazów tych okręgów, to funkcja (2) odwzorowuje wnętrze każdego z danych okręgów na zewnętrze odpowiedniego obrazu.

Okrąg \z—3| = 9 leży wewnątrz okręgu \z— 8| = 16, wobec tego promień obrazu okręgu \z— 3| = 9 jest większy niż promień obrazu okręgu \z— 8| = 16. Zgodnie z warunkami zadania nieznany współczynnik k we wzorze (2) należy tak dobrać, aby dla punktów okręgu |z— 3| = 9 było |w| = 1. Weźmy np. pod uwagę punkt z = 12, leżący na okręgu |z-3| = 9. Przyjmując z = 12 we wzorze (2>, otrzymujemy 12+24

12 ’

w = 3 k.

Wobec tego, że ma być |w| = 1, otrzymujemy

|3fc| = 1.

Stąd natychmiast

(3)    fc=y,

gdzie a jest dowolną liczbą rzeczywistą.

stosujemy wzór (1)

W naszym zadaniu /(z) = z /'(*) = 2z Wobec tego zgodnie ze wzo s-1(4(1“

D

W celu obliczenia długości . ⁽²)

gdzie z = z(/),    j<