P1080527 (2)

20

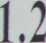
Modele szeregów czasowych z tendencją rozwojową

Modele

analityczne

1.2.1

Modele analityczne stosuje się do prognozowania zjawisk, które charakteryzowały się w przeszłości regularnymi zmianami, dającymi się opisać za pomocą funkcji czasu i wobec przyszłego rozwoju których przyjęto postawę pasywną. Zakłada się nie tylko niezmienność kierunku trendu (rosnący, malejący), ale również stałość charakteru zmian zjawiska wyrażoną przez niezmienność postaci analitycznej funkcji trendu (liniowa, potęgowa, logarytmiczna itd.) i oszacowanych parametrów strukturalnych modelu Przy budowie prognoz wykorzystuje się regułę podstawową (prognozy krótkookresowe) lub regułę podstawową z poprawką (prognozy średniookresowe).

Wyboru postaci analitycznej modelu dokonuje się na podstawie przesłanek teoretycznych dotyczących mechanizmu rozwojowego prognozowanego zjawiska, oceny wzrokowej wykresu przeszłych wartości zmiennej oraz dopasowania modelu trendu do danych empirycznych. Do oceny dopasowania modelu do wartości rzeczywistych zmiennej prognozowanej można się posłużyć a) współczynnikiem determinacji

R

ib.-r?

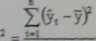
, R¹ e [0,1],

21

b) standardowym błędem oceny modelu

⁵⁼tw    1

gdzie: y, - rzeczywista wartość zmiennej Y w momencie/okrcsie t,

y_t - teoretyczna wartość zmienny Y wynikająca z modelu, w momencie/okresie t,

y    - średnia wartość zmienny Y w szeregu czasowym o długości n,

m - liczba zmiennych objaśniających modełu,

—łiczba parametrów mudetu, =>

Przyszłą wartość zmiennej (prognozę punktową) uzyskuje się przez ekstrapolację funkcji trendu, czyli przez podstawienie do modelu w miejsce zmiennej czasowej numeru momentu/okresu T, na który wyznacza się prognozę:

rWC*)

Do oceny dopuszczalności zbudowanych prognoz używa się błędów ex antę:

a) dla modełu liniowego

’S ,

Kt-i? “

. M    J

b) dla modeli nieliniowych sprowadzalnycfa do liniowych

j&rt ’

ll#J

gdzie: Y* - zmienna określona transformacją liniową Y^F=f(Y),

(jy*

pochodna — jest liczona w punkcie y_T,

«y

v| - wariancja prognozy dla zmiennej Y w momeacie/okresie T, - wariancja prognozy dla transformaty Y* w momenci e/ofcre-sie T (zob. pkt 2.1).