ras z412

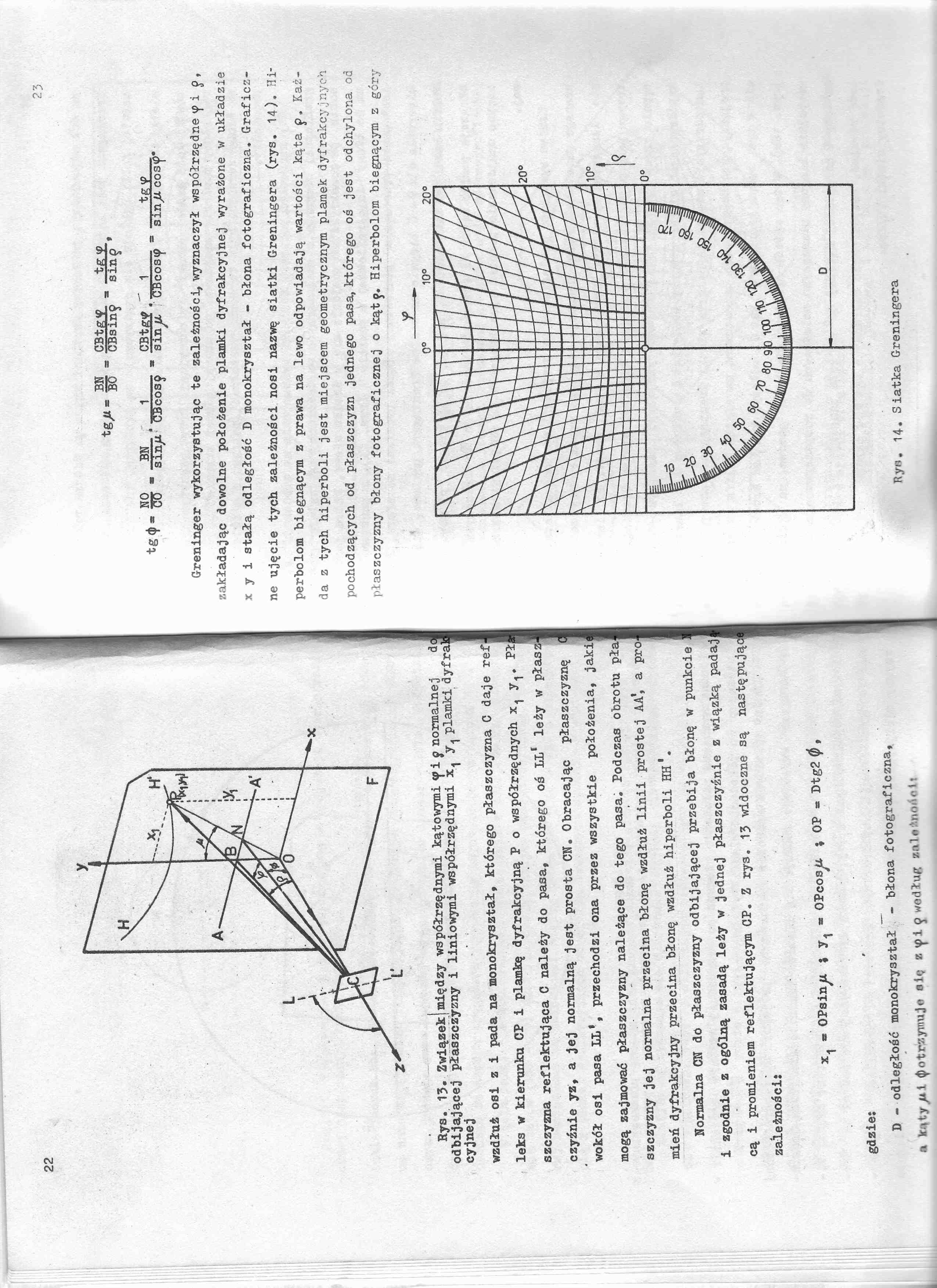
Rys. 13. Związeklmiędzy współrzędnymi kątowymi<pij normalnej dc odbijającej płaszczyzny i liniowymi współrzędnymi x, y. plamki dyfrai cyjnej

wzdłuż osi z i pada na monokryształ, którego płaszczyzna C daje refleks w kierunku CP i plamkę dyfrakcyjną P o współrzędnych x₁ y^. Pł szczyzna reflektująca C należy do pasa, którego oś LI¹ leży w płasz czyźnie yz, a jej normalną jest prosta CK. Obracając płaszczyznę ( wokół osi pasa ŁŁ¹, przechodzi ona przez wszystkie położenia, jaki mogą zajmować płaszczyzny należące do tego pasa. Podczas obrotu pła szczyzny jej normalna przecina błonę wzdłuż linii prostej AA¹, a pro mień dyfrakcyjny przecina błonę wzdłuż hiperboli HH¹.

Normalna CK do płaszczyzny odbijającej przebija błonę w punkcie 1 i zgodnie z ogólną zasadą leży w jednej płaszczyźnie z wiązką padaj cą i promieniem reflektującym CP. Z rys. .13 widoczne są następują^ zależności:

x^ = OPsin^i i y^ « OPcos^t ; OP = Dtg2 (f),

gdzie:

D - odległość monokryształ - błona fotograficzna, a kąty^i 1 <})otrlzymuje olg zipię według zalnżnodolt

.    . BN CBtg«P

_i£J£

sinp

*«/*■ W " GBsinę

NO

TO

BN 1 siną CScosf

CBtgf 1    tgy

singli CBcosj ^- sm/icosj*

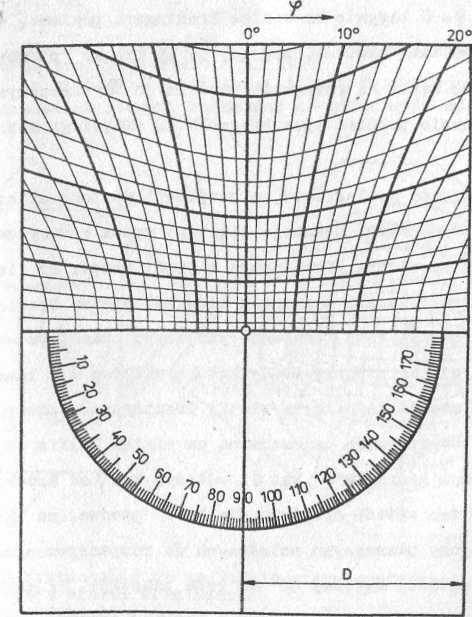
Greninger wykorzystując te zależności, wyznaczył współrzędnej! p, zakładając dowolne położenie plamki dyfrakcyjnej wyrażone w układzie x y i stałą odległość D monokryształ - błona fotograficzna. Graficzne ujęcie tych. zależności nosi nazwę siatki Greningera (rys. 14). Hiperbolom biegnącym z prawa na lewo odpowiadają wartości kąta p. Każda z tych hiperboli jest miejscem geometrycznym plamek dyfrakcyjnych pochodzących od płaszczyzn jednego pasa, którego oś jest odchylona od płaszczyzny błony fotograficznej o kąty. Hiperbolom biegnącym z góry

20°

10°

<?

0°

Ryn. 14. Siatka Greningera