ras z419

(8)

■}ó

f (x)=»y A cos nTTx + 22 ^B sin n1Tx, ^N ' n ⁿ    n. ⁿ

(8)

■}ó

zaś odbywa się po wszystkich dodatnich i ujemnych liczbach całkowitych n.

Równaniem całkowicie równoważnym z (8) jest:

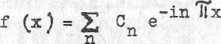
(.9)

gdzie:

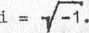
Równania (8) i (9) są równoważne, gdyż wyrażenie potęgowe w równa-niu (9j może być wyrażone funkcjami trygonometrycznymi:

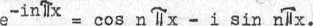
Funkcja gęstości elektronowej wyrażona szeregiem Fouriera ma postać:

P(xyz)=4- ZSZ F_h,-,exp[-2Tii(hx + ky + lz)],    (10)

>    "V h k 1 ⁿ

adzie    są współczynnikami tego szeregu; h,k,l są liczbami całko

witymi, po których szereg je3t sumowany, a - objętością komórki e» lementamej. Ze względu na trójwymiarową periodycznośó wymagane je3t potrójne sumowanie.

Amplituda struktury może być w ogólnym przypadku liczbą zespoloną w postaci: •

^Phkl ^{= A}hkl ^{+ 1 B}hkl-

Biorąc to pod uwagę, można wzór (.10) zapisać w postaci: «dz le:

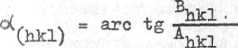
p(xyz) -    2 Z Z |P_hlcl| oon[?'II’(hx + ky + |lz)- o(fa_klO. (11)

K h k 1    '    *

W przypadku gdy w krysztale iistnie je środek symetrii, wówczo.

^,Phkl " ^Ahkl * ^Bhkl = °* °W-|) = ⁰ 1 wzór (11) Przyjmuje postać:

ip(xyz)= 2 £ 2 F_hklcos2TT(hx + ky +!lz).

h k 1

(12)

Wstawiając do równania (10) wartości amplitud struktury F,, . jat , współczynniki szeregów Fouriera, można obliczyć w każdym punkcie i;- -mórki elementarnej gęstość elektronową. W praktyce dzieli się komórkę elementarną wzdłuż osi na określone odcinjki wyznaczające punkty pomiarowe i oblicza dla nich gęstość elektronową. W przypadku trójwymiarowej syntezy Fouriera i podziału każdej z trzech osi na 100 i-, ' ■;

oinkow uzyskano by 100 , a więc milion punktów obliczeniowych. Jest to praco- i czasochłonne nawet z zastosowaniem dużych maszyn licsą-■ych. Czasem więc wystarczające jest wykonanie kilku projekcji gęstości elektronowej na płaszczyznę prostopadłą do określonego kierunku krystalograficznego.

Jako wynik syntezy Fouriera otrzymuje się dla każdego punktu pomiarowego wartość liczbową obrazującą gęstość elektronową. Łącząc pun-I'ty o jednakowej wartości gęstości elektronowej, uzyskuje się graficzny obraz przypominający mapę z warstwicami, który umożliwia doli ładne określenie współrzędnych atomu. Istotnym założeniem w synte-■le Fouriera jest znajomość amplitud struktury. Zwykle, szczególnie

w początkowych stadiach badań, nie jest to spełnione. Z natężenia rc-

p

fleksów uzyskuje się bowiem czynnik struktury    natomiast kąt fazowy    ^{a nawe}'^t znak amplitudy struktury w przypadku struktur ::<

'rodkiem symetrii, nie są znane. Chcąc więc prowadzić analizę strukturalną za pomocą szeregów Fouriera, należy znać kąt fazowy ot lub w