13463 Scan20003 (2)

Szeregi liczbowe

Sereg harmoniczny rzędu a (wykorzystuje się w kryterium porównawczym)

El    a < 1 szereg rozbieżny

n^a    a > 1 szereg zbieżny

Kryteria zbieności szeregów

1.) Kryterium d’Alemberta

lim

n—>■ oo

&n+1

0>n

= 9,

g < 1 szereg zbieżny g > 1 szereg rozbieżny

2.) Kryterium Cauch’ego

lim    = ^

n—>oo

{g < 1 szereg zbieżny (/ > 1 szereg rozbieżny

3a.) Kryterium porównawcze 1

0 < a_n < b_n dla wszystkich n > N, N ustalone

to jeżeli Y b_n jest zbieżny to szereg Y ^an jest też zbieżny. Jeżeli Y ^an jest rozbieżny to szereg Y bn jest też rozbieżny. 3b.) Kryterium porównawcze 2

lim

n—>-oo

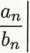
— k, k G (0, oc)

Szeregi Y ^an i Y b_n są równocześnie zbieżne albo rozbieżne 4.) Kryterium całkowe

/ :< 1, oo) i—> R jest ciągła , malejąca i dodatnia,

caka niewłaściwa

OO

/

OO

f{x) dx i szereg } _y f(n),

n—1

są równocześnie zbieżne albo rozbieżne.

5.) Kryterium Leibniza (dla szeregów naprzemiennych) Jeżeli ciąg {a_n} jest nierosnący i lim a_n = 0, to

n—7 oo

szereg naprzemienny E (-l)ⁿa_n jest zbieżny i |i2n| < a_n+1 Kryterium Weierstrassa (dla szeregów funkcyjnych

Jeeli istnieje ciąg liczbowy {6_n} taki, że \/x G A, Mn G N\f(x) < b_n i szereg Y b_n jest zbieżny to

szereg funkcyjny 5^/_n(x)jest zbieżny jednostajnie w A i bezwzględnie

Szereg potęgowy

OC

52 ^ttn

71=1

promień zbieżności szeregu potęgowego

r — lim

n—yoo

&n+1

tzn. dla jx| < r szereg jest zbieżny, dla |x| > r rozbieżny

Twierdzenia o cołkowaniu i różniczkowaniu szeregu funkcyjnego

Jednostajnie zbieżny szereg funkcji ciągłych na przedziale < a, b > ma sumę ciągłą

taki szereg można całkować wyraz po wyrazie,

Jednostajnie zbieżny szereg funkcji ciągłych i różniczkowalnych na przedziale < a, b>

można różniczkować “wyraz po wyrazie”, o ile szereg pochodnych jest jednostajnie zbieżny na < a, b >

1