39360 str210

210 4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO i 2. KLaSYI

Zadania przykładowe

Zadanie 2.1. Wyznaczyć obszar, w którym równanie różniczkowe

(1)

d²u d²u    , d²u du

—ij-3y-_a—•+(9-x²)—₂ + x- = 0

dx² dxdy    oy²

jest typu eliptycznego.

Rozwiązanie. Obliczamy 5 = B²—4AC:

S = 9y²-4(9-x²) = 4x² + 9y²-36.

Równanie (1) jest typu eliptycznego dla tych x, y, dla których ó<0. Mamy zatem

2 2

4x² + 9y² —36<0,    —<1. ''

9    4

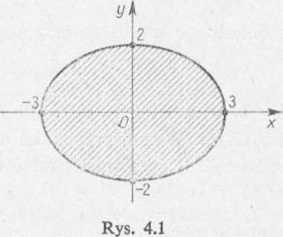
x² y²

Szukanym obszarem jest wnętrze elipsy o równaniu —+ — ⁼ I (patrz rys. 4.1).

Zadanie 2.2. Wyznaczyć obszar, w którym równanie różniczkowe

Zadanie 2.3. Sprowadzić < d²ti

(1)    3p⁺4c°^:

Rozwiązanie. Obliczani] d = B²-*

Równanie (1) jest zatem ty charakterystyk

skąd mamy

(2)

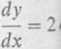
Rozwiązania równań (2) (

y —sini

Dla sprowadzenia równań (1} nych ć, i ą (2.12) określonych

t = y-

Obliczamy obecnie współc; po przejściu do zmiennych l;

B, = 2 A

(1)

4

ćfu

dx²

+(x-y + l)

d²u d²u    du

T~r⁺T~2~xy —

dxdy dy    dy

jest typu hiperbolicznego.

Rozwiązanie. Obliczamy <5 = B²—4AC:

<5 = (x —y + 1)² —16.

Równanie (1) jest typu hiperbolicznego dla tych wszystkich punktów M(x,y), dla których <5>0. Mamy stąd następującą nierówność:

(2)    (x —y + 1)² —16>0.

/

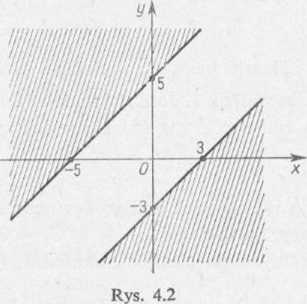
Nierówność (2) jest spełniona dla wszystkich punktów M(x,y) leżących w następujących półpłaszczyznacli (patrz część zakreskowana na rys. 4.2):

y<x— 3 lub    y>x + 5.

dx dx \dx = 2 (4 cos² 2,v—4)+'

a, = A

= 4

b_x — A = 4

We współrzędnych £ i i;

14*