DSC04654

ru/ywmm funkcjonałem kwadratowym. jadł jcsl ona funkcjonałem kwadratowym _y znaczonym przez pewien funkcjonał dwulmiowy symetryczny określony na pr/r^j,, ni V

Jeśli jest funkcjonałem kwadratowym na przestrzeni V , to istnieje dokładnie joj,, funkcjonał dwulmiow y symetryczny v>. który wyznacza 0.

Jeśli 5 a (i'i.. . «J jest baza przestrzeni wektorowej V'. to funkcja 0 . V K jest funkcjonałem kwadratowym wtedy i tylko wtedy, gdy istnieje układ skaUf-_/t

. ji|. »ki^K <*tf ® ty <Błi, i € (I.....n| oraz

4*... 4- x*t>«) = } y^ajjX/Xj. '=1 y=i

Wielomian zmiennych .xj.....i„ stojący po prawej stronie równości (7.6 j na/ywin

formą kwadratową funkcjonału 0 w bazie 8. natomiast macierz symetryczną |o < M(«. AM nazywamy macierzą funkcjonału kwadratowego 0 w bazie 8

Rząd macierz) funkcjonału kwadratowego 0 w bazie 8 przestrzeni wektorowe , nie zależy od wyboru bazy 8 Rząd ten nazywamy rzędem funkcjonału kwadratowego#

Barę 8 skończenie wymiarowej przestrzeni wektorowej V nazywamy bazą Lin.. mczną funkcjonału kwadratowego 0 określonego na przestrzeni V. jeśli macierz runi cjorulu 0 w tej bozie jest diagonalna.

TWIERDZENIE La<;raNGE*A. Każdy funkcjonał kwadratowy określony na " ■ czenic wymiarową} przestrzeni V ma bazę kanoniczny.

Przykład 94. Funkcjonał kwadratowy 0 na przestrzeni wektorowej R^: okleiło* jest wzorem $(|xi.x₂j) = x_l³ 4 8x1X2 + 5x₂. Znaleźć funkcjonał dwuliniowy syn* tiyczny \p wyznaczający funkcjonał kwadratow y 0 i wskazać macierz funkcjotulu i w bazie kanonicznej przestrzeni R\

Roz*'ią&nie. Aby otrzymać formę funkcjonału *p. wystarczy składniki x\ i 5i: a-stąpić składnikami *|>i i Sxjyi waz składnik Śxix₂ zastąpić sumą 4.t,yt4-4x»y, W mku otrzymujemy wzór y>(Jx,. x₂). ty», y^j) = Xjyj 4- 4xjyz 4- 4xi>'t 4- 5xjyj.

Macierzą funkcjonału 0 jest macierz funkcjonału dwuliniowego symetrycznego;

wyznaczającego funkcjonał 0. czyli macierz

Przykład 95. Stosując metodę Lagrange’a. znaleźć bazę kanoniczną 81 odpowie* mą formę kanoniczną funkcjonału kwadratowego 0 określonego na przestrzeni wcU> rowej R^j wzorem

a)    4><{x,,xj.x>D ss x* -F2xJ 4-3xJ 4- 2x,x₂ 4-4xjX3 4- 5x₂.t3.

b)    $<(xi.x₂.X}]) = X|Xs - 5xix₅ 4- 7x₂x₃.

Rozwiązanie. Ad a) Grupując wszystkie składniki, w których występuje op ¹ otrzymujemy

0(v) s (xf lc,x₂ 4- 4xjXj) 4- 2xl ⁺ 3x| 4* 5x₂xj

= (x, 4- x> 4- 2xj)² - U₂ 4- 2x,r 4- 2x| 4- 3xj 4- 5x>x, * (X| 4- x₂ 4- 2x»r 4- x\ - x² 4- x₂xj.

fi buic. w której współrzędnymi są y,. >j. >funkcjonał« _m l(jOBę

Dalsze przekształcenia przebiegają następująco:

<p(v) = yf + {yj + yjy,) - y>

= y? + (y: ♦ taf - (5*)^: - jś ■ y?+(*+ś*)² - \yi

Wobec tego nowe współrzędne li. 2j. *j wprowadzamy a pomocą wtórów

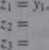
Oprowadzamy teru/, nowe współrzędne wzorami

>1 + 3*.

Ty

W tej bazie przestrzeni R³. w której współrzędnymi są ;₃, funkcjonał $ ma formę <X»(u) = -f-hsf —

Żalem baza ta jest bazą kanoniczną funkcjonału <P Aby wyznaczyć wektory tej buzy. ijnrimy wyjściowe współrzędne jt|. *j. x₃ przez współrzędne&

*y = V3 = 2,.

Niech 5 = U'i. ih. t’j). Ponieważ ciągami współrzędnych wektorów r,. i-. n w bazie 5 są odpowiednio ciągi (1,0.0), (0.1.0) i (0.0.1 i. więc zachodzą rtwnoici ti = [1.0.0|.    = [-1. I. Ol, t>j = (-5. Ij. Dokonując bowiem we wzorach 17.7 (pod-

wwień Z\ ►— 1. Z2 *-* 0. 2, *-+ O. otrzymujemy współrzędne wektora e, w bazie baonicznej przestrzeni R\ Podobnie podstawienia :i h* 0.<-* I. z — u oraz -*i *- 0. Z} *— 0. i3 >-* I po/w alają wyznaczyć współrzędne wektorów ej i v\ w tonę bnontczncj przestrzeni R³.

Odpowiedi Na przykład B = (fl.0.01. (-1.I)» i wówczas mamy

♦(ftd.o. 01+22!—I, i.0] + -i U)«4+Ą - H

Ad b). Ponieważ w danej formie kwadratowej nie występuje kwadrat radnej re zmiennych X\, xj. *3. więc możemy zastosować podstawienie

-*1 = >i + yj.

•*2 = vi - yi. xj ~    Ti-