KINEMATYKA

Bryła sztywna - jest to ciało, w którym odległości Pomiędzy poszczególnymi punktami nie ulęgają zmianie. Położenie ciała względem nieruchomego układu odniesienia można określić podając położenie trzech wybranych punktów tego ciała nie leżących na jednej prostej.

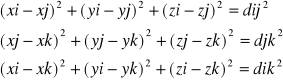
Ruch postępowy ciała sztywnego:

Równolegle przesuniecie ciała sztywnego względem układu odniesienia nazywamy ruchem postepowym. Każdy punkt wykonuje przesuniecie równolegle zwane translacja.

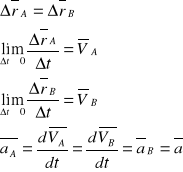
Ruch obrotowy bryły sztywnej:

Ruch obrotowy nazywamy taki ruch, w którym dwa punkty tego ciała są nieruchome. Przechodzące przez te punkty prosta nosi nazwę osi obrotu. Wszystkie punkty ciała leżące na tej prostej są nieruchome natomiast pozostałe zataczają okręgi o środku leżącym na osi.

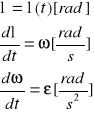
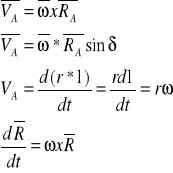
Przyspieszenie w ruchu obrotowym:

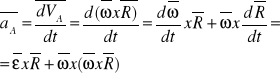
Ruch plaski bryły sztywnej:

Ruchem płaskim nazywamy taki ruch ciała, w którym wszystkie punkty przemieszczają się równolegle do pewnej płaszczyzny zwaną płaszczyzną kierująca. Wystarczy znać ruch przekroju dowolnego bryły sztywnej, aby określić ruch całej bryły.

Metody wyznaczania prędkości brył sztywnych w ruchu płaskim:

1.)Metoda rzutów prędkości - oparta jest na twierdzeniu Shalla. Rzuty prędkości dwóch punktów ciała sztywnego na prosta łączącą te punkty są sobie równe.

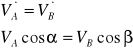
2.)Metoda superpozycji - oparta jest na opisie ruchu w postaci translacji i obrotu.

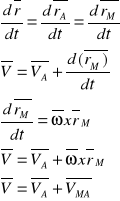
3.)Metoda chwilowego środka obrotu - oparta jest na ustawieniu ruchu płaskiego w postaci obrotu. Obrót ten odbywa się wokół chwilowego środka obrotu.

W układzie nieruchomym miejsce geometryczne chwilowych środków prędkości nazywamy centroidą nieruchomą, a w uk. Ruchomym związanym z poruszającym się ciąłem nazywamy centroida ruchoma.

Chwilowym środkiem prędkości nazywamy taki punkt przekroju ciała, dla, którego prędkość liniowa w danej chwili jest równa 0.

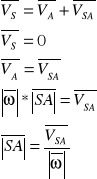
Przyspieszenie w ruchu płaskim:

Wyznaczanie przyspieszenia metoda superpozycji:

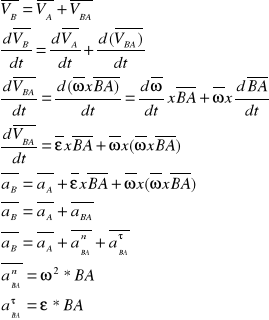
Metoda chwilowego środka przyśpieszeń:

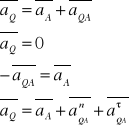
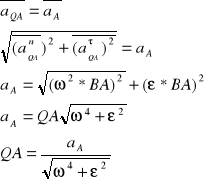
Ruch kulisty bryły sztywnej:

Ruchem kulistym bryły sztywnej ciał sztywnego nazywamy taki ruch ciała sztywnego, którego 1 punkt zwany środkiem ruch kulistego jest nieruchomy zaś torami pozostałych punktów jest powierzchnia kuli ośrodku w punkcie. Ruch kulisty opisujemy za pomocą tzw. kątów Eulera.

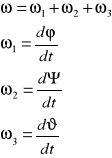
Ruch kulisty jest chwilowym ruchem obrotowym wokół osi przechodzącej przez środek ruchu kulistego.

Ponieważ położenie chwilowego środka obrotu nie zmienia się miejscem geometrycznym kolejnych położeń osi jest stożek.

Miejsce geometryczne kolejnych położeń osi w układzie nieruchomym nazywamy aksoida stała w układzie ruchomym aksoida ruchoma.

Precesja regularna:

Przypadek ruchu kulistego, w którym kat nutacji jest stały a wartość prędkości kątowej obrotu własnego i precesji tez są stale nazywamy precesja regularna.

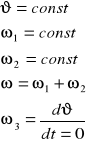
Przyspieszenie w ruchu kulistym:

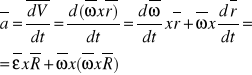
Przyspieszenie w precesji regularnej:

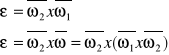
Ruchu złożony:

W zależności od układu odniesienia względem, którego badamy ruch mamy odczynienia z ruchem względnym i bezwzględnym.

Ruch ciała względem nieruchomego ciął w układzie odniesienia nazywamy ruchem bezwzględnym.

Ruch ciała względem ruchomego układu odniesienia nazywamy względny.

Ruch układu ruchomego względem nieruchomego ciała nazywamy ruchem unoszenia.

Prędkość w ruchu względnym{złożonym}:

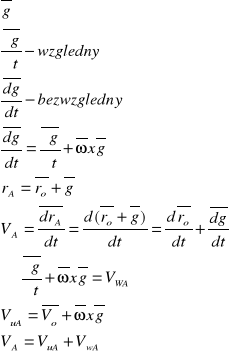
Przyspieszenie w ruchu złożonym:

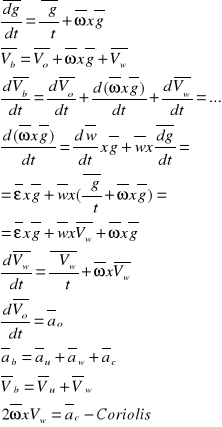
DYNAMIKA

Środek masy punktu materialnego:

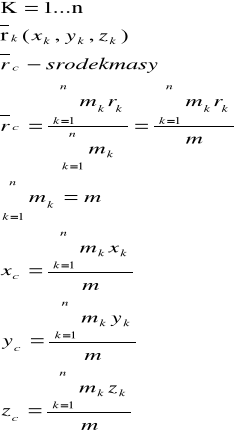
Zasada pędów układu punktów materialnych:

Pęd uk. Punktów materialnych jest równy iloczynowi masy wszystkich punktów i prędkości środka masy układu punktów materialnych.

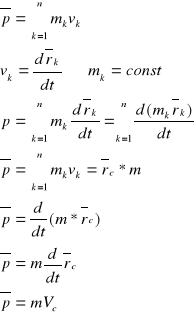
Zasada ruchu środka masy.

Pochodna pędu jest równa sunie sil się wewnętrznych działających na układ w danym czasie.

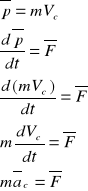
Środek masy punktów porusza się tak jakby w nim skąpione były wszystkie siły działające na układ punktów.

DYNAMIKA BRYLY SZTYWNEJ

Moment bezwładności:

Momentem bezwładności ciała względem osi nazywamy granice, do której dąży suma iloczynów mas i kwadratów odległości od danej osi.

Moment bezwładności względem osi jest równy sumie momentów bezwładności względem dwóch wzajemnie prostopadłych płaszczyzn przecinających się wzdłuż tych osi, natomiast biegunowy moment bezwładności równy jest sumie momentów bezwładności względem trzech wzajemnie prostopadłych płaszczyzn przecinających się w biegunie albo połowie sumy momentów bezwładności względem trzech prostopadłych do siebie osi poprowadzonych z bieguna.

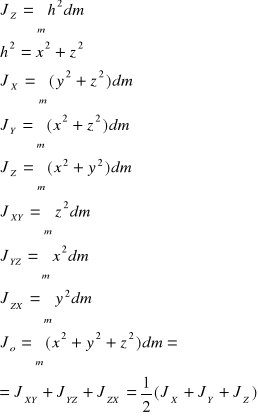
Tw. Stinera

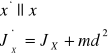
Momenty dywinacji

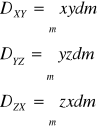
Dynamiczne równanie ruchu postępowego bryły sztywnej.

Jeżeli wypadkowa sil się zewnętrznych będzie leżała na tej samej lini działania, co siła bezwładności ma wówczas bryła sztywna porusza się ruchem postępowym będzie w równowadze

---