Grupa W106

Piotr Naglik

Jan Omorczyk

Dariusz Pochopień

Piotr Smutrykowski

Ćwiczenie 56

Temat: Badanie wpływu temperatury na przewodnictwo elektryczne ciał stałych.

Opór elektryczny przewodników w temperaturach dużo wyższych od temperatury Debye'a rośnie liniowo wraz ze wzrostem temperatury:

(1)

gdzie: Ro - opór elektryczny przewodnika w temp. otoczenia,

ΔT - przyrost temperatury,

α - temperaturowy współczynnik oporności elektrycznej.

Dla przewodnika w tym zakresie temperatur opór elektryczny maleje eksponencjalnie ze wzrostem temperatury:

(2)

gdzie: E - szerokość pasma wzbronionego,

k - stała Boltzmana,

Rpo - stała oporności zależna od koncentracji nośników ładunku
w stopniu podstawowym i ich ruchliwości.

Logarytmując obustronnie równanie (2) otrzymujemy liniowe zależności lnR od odwrotności temperatury w skali bezwzględnej 1/T [K-1]

(3)

Wyznaczając parametry prostej korelacji y=ax+b dopasowanej do eksperymentalnego wykresu funkcji:

  1. R / Ro=f (ΔT) (dla przewodnika) temperaturowy współczynnik oporności obliczyć można z wartości współczynnika kierunkowego tej prostej,

  2. ln R=f (1/T) (dla półprzewodnika) szerokość pasma wzbronionego E dla badanego półprzewodnika obliczyć można z wartości współczynnika kierunkowego tej prostej. Jego wartość jest bowiem równa E/k. Wyraz stały prostej korelacji jest równy natomiast wartości ln Rpo.

TABELA POMIAROWA:

PRZEWODNIK

t [oC]

ΔT [K]

R [Ω]

ΔR

R/Ro

25

0

18,0

1,80

1

30

5

18,2

1,82

1,011

35

10

18,5

1,85

1,028

40

15

18,7

1,87

1,039

45

20

19,1

1,91

1,061

50

25

19,4

1,94

1,078

55

30

19,8

1,98

1,100

60

35

20,2

2,02

1,122

65

40

20,5

2,05

1,139

70

45

20,9

2,09

1,161

75

50

21,2

2,12

1,178

80

55

21,6

2,16

1,200

PÓŁPRZEWODNIK

T[K]

1/T [K-1]

R [kΩ]

ΔR [kΩ]

Ln R

298,15

0,0034

8,78

0,878

2,17

303,15

0,0033

6,99

0,699

1,94

308,15

0,0032

5,65

0,565

1,73

313,15

0,0032

4,43

0,443

1,49

318,15

0,0031

3,62

0,362

1,29

323,15

0,0031

2,98

0,298

1,09

328,15

0,0030

2,48

0,248

0,91

333,15

0,0030

2,07

0,207

0,73

338,15

0,0029

1,75

0,175

0,56

343,15

0,0029

1,50

0,150

0,41

348,15

0,0028

1,29

0,129

0,25

353,15

0,0028

1,12

0,112

0,11

Wykorzystując program komputerowy obliczamy współczynniki kierunkowe prostych R/Ro=f (ΔT) - dla przewodnika i lnR=f (1/T) dla półprzewodnika:

PRZEWODNIK: PÓŁPRZEWODNIK:

a= 0,003765 a= 3964,519

b= 0,990000 b= - 11,1515

Wartość pasma wzbronionego półprzewodnika obliczamy z zależności:

E=a ⋅ k

gdzie:

k - stała Boltzmana

a - współczynnik kierunkowy prostej lnR = f (1/T)

E= 3964,519 K ⋅ 8,617342⋅10-5 eV/K = 0,34 eV

E=0,34 eV

PRZEWODNIK

PÓŁPRZEWODNIK

R/Ro

Rpo [kΩ]

Rpo [kΩ]

E/k [K]

E [eV]

1

2,667

0,036

3964,519

0,34

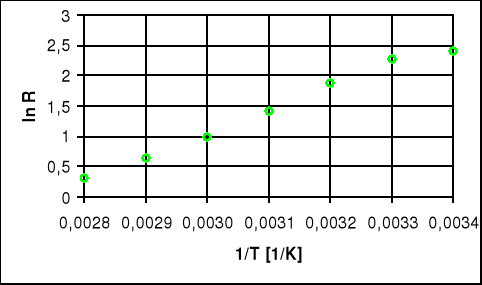
0x08 graphic
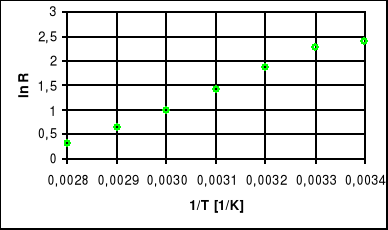
Wykres lnR=f(1/T) - dla półprzewodnika

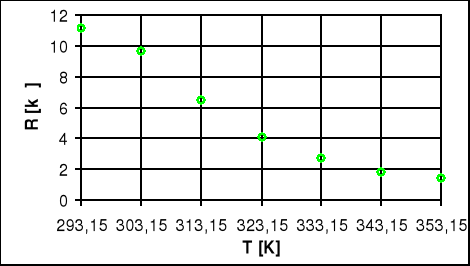
0x08 graphic
Wykres R=f(T) - dla półprzewodnika

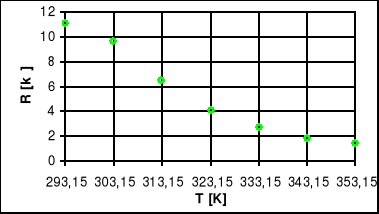
0x01 graphic

0x01 graphic