LABORATORIUM FIZYKI			ĆWICZENIE: 32
			DATA:
Wydział:	Grupa:	Zespół:	Punktacja:	Przygotowanie:
Nazwisko i imię:
Temat ćwiczenia: Badanie korelacji liniowej pomiędzy prądem i napięciem w obwodzie elektrycznym					Sprawozdanie:
Prowadzący:					Suma punktów:

WSTĘP

Celem cwiczenia jest wyznaczenie modułu piezoelektrycznego d metodą statyczną. Cwiczenie to ma na celu zapoznanie się ze zjawiskiem piezoelektrycznym oraz własnościami piezoelektryków i ich wykorzystaniu w technice.

Występują dwa znane zjawiska piezoelektryczne. Efekt piezoelektryczny prosty i efekt piezoelektryczny odwrotny. Polaryzacje elektryczną wywołaną mechanicznym naprężeniem nazywa się prostym zjawiskiem piezoelektrycznym, a odkształcenie ciałą pod wpływem przyłożonego napięcia elektrycznego odwrotnym zjawiskiem piezoelektrycznym.

Efekt piezoelektryczny prosty

gdzie

P- polaryzacja

d - moduł piezoelektryczny

T - naprężenie

Efekt piezoelektryczny odwrotny

S= d * E gdzie

S - odkształcenie

D - moduł piezoelektryczny

E - napięcie pola elektrycznego

Moduł piezoelektryczny jest stosunkiem odkształcenia do napicia pola elektrycznego albo stosunkiem naprężenia do wywołanej polaryzacji.

d=

UKLAD POMIAROWY, WYKONANIE CWICZENIA

Cwiczenie składało się z dwóch części.

Pierwsza częśc polegała na wyznaczeniu stałej balistycznej galwanometru.

Galwanometr służy do pomiarów przepływającego ładunku. Parametrem opisującym działanie galwanometru jest stałą balistyczna b , która jest współczynnikiem proporcjonalności miedzy wskazaniem galwanometru a wartością przepływającego ładunku. Ponadto układ pomiarowy składał się z zasilacza, woltomierza, kondensatora i przełącznika. Kondensator miał pojemnośc 5000pF.

Na początku wykonano 10 pomiarów. Zmieniając napięcie co 1 [V] odczytywano z galwanometru wychylenie w działkach [dz]. Następnie po zmianie polaryzacji napięcia na przeciwną wykonano także 10 pomiarów ponownie, również zmieniając napięcie co 1[V].Wówczas wskaźnik wychylał się w przeciwna stronę.

Druga częśc cwiczenia polegała na pomiarze modułu piezoelektrycznego d w zjawisku piezoelektrycznym prostym. Układ został podłączony do galwanometru. Wykonano 6 pomiarów dodając kolejno po sześc ciężarków , każdy o masie 0,5 [kg] zmieniano obciążenie główne. Przemieszczając rączkę blokady odczytano maksymalne wychylenia plamki galwanometru. Po zmianie polaryzacji również wykonano 6 pomiarów w identyczny sposób. Wówczas wskaźnik wychylał się w przeciwną stronę.

Należy zaznaczyc, że odczyt z galwanometru był trundy z powodu szybkiego poruszania się wskaźnika.

WYNIKI ,ICH OPRACOWANIE I RACHUNEK BŁĘDU

Pierwsza częśc cwiczenia.

Znając pojemność kondensatora C obliczono ładunek zgromadzony na jego okładkach dla każdego napięcia według wzoru

Lp	Napięcie [V]	Ładunek [C]	Wychylenie [dz]
1	1	0,5 x 10^-8	4
2	2	1,0 x 10^-8	9
3	3	1,5 x 10^-8	13
4	4	2,0 x 10^-8	18
5	5	2,5 x 10^-8	22
6	6	3,0 x 10^-8	26
7	7	3,5 x 10^-8	30
8	8	4,0 x 10^-8	35
9	9	4,5 x 10^-8	39
10	10	5,0 x 10^-8	45

Po zmianie polaryzacji napiecia na przeciwną strona wynik były następujące:

Lp	Napięcie [V]	Ładunek [C]	Wychylenie [dz]
1	1	0,5 x 10^-8	5
2	2	1,0 x 10^-8	9
3	3	1,5 x 10^-8	14
4	4	2,0 x 10^-8	19
5	5	2,5 x 10^-8	24
6	6	3,0 x 10^-8	28
7	7	3,5 x 10^-8	32
8	8	4,0 x 10^-8	36
9	9	4,5 x 10^-8	41
10	10	5,0 x 10^-8	45

Według wzoru
gdzie

q- ładunek zgromadzony na okładkach kondensatora

- wychylenie wskaźnika świetlnego galwanometru

b- stała balistyczna galwanometru

Stosując program ORIGIN wyznaczono metodą najmniejszej sumy kwadratów stała galwanometru b. Ilustruje to wykres ładunku q [C] od wychylenia alfa [dz]

Stała balistyczna b = 1,12485*10^-8 a jej bład przypadkowy ∆bp1=9,61418*10^-10

Współczynnik t-Studenta

t = (0,99;8) = 3,36

Β=0,99 k= n-2 = 8 więc

∆bp= (∆bp1 * t)= 9,61418*10^-10 * 3,36 = 3,3*10^-9

Błąd pomiaru ładunku q= C*U

Przyjęto, że niepewnośc ładunku zgromadzonego na kondensatorze wynosi

∆C=0 więc U*∆C=0

Błąd systematyczny woltomierza:

Więc

∆U= 0.3 [V]

Zatem błąd systematyczny pomiaru ładunku

[C]

Z uwagi na wspomniany już ciężki odczyt z galwanometru przyjęto, że błąd odczytu wynosi 3 działki

Błąd systematyczny stałej balistycznej policzono ze wzoru:

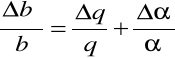
q- przyjmuje pomiar nr. 5 =2,5 x 10^-8

- przyjmuje z pomiaru nr. 5 = 24

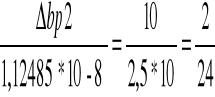
1,12485*10^-8 * 0,4 =4,99*10^-9

Ostatecznie bład całkowity stałej balistycznej wyznaczono wykorzystując prawo przenoszenia błędów. Bł. Przypadkowy ∆bp1=9,61418*10^-10 Bł. Systematyczny
4,99*10^-10

Błąd średni kwadratowy pomiaru:

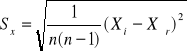
Sx=0,13

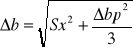
∆b=1,3x10^-9
Ostateczny wynik : b = (1,12*10^-8 ± 0,13 * 10^-8 )

^{Druga częśc cwiczenia}

^{Wyniki pierwszej serii pomiarów}

^Lp	^Obciążenie m[kg]	^Siła nacisku [F]	^Wychylenie [dz]	^Ładunek [C]
^1	^0,5	^53,95	^9	^1,008 x10^-7
^2	^1,0	^107,91	^15	^1,512 x10^-6
^3	^1,5	^161,86	^20	^3,024 x10^-5
^4	^2,0	^215,82	^25	^7,56 x10^-4
^5	^2,5	^269,77	^31	^1,874 x10^-4
^6	^3,0	^323,73	^34	^3,808 x10^-7

^{Druga seria pomiarów}

^Lp	^Obciążenie m[kg]	^Si^ła nacisku F [N^]	^Wychylenie [dz]	^Ładunek [C]
^1	^0,5	^53,95	^13	^1,456 x10^-7
^2	^1,0	^107,91	^15	^1,68^x10^-7
^3	^1,5	^161,86	^20	^2,24 x10^-7
^4	^2,0	^215,82	^27	^6,048 x10^-7
^5	^2,5	^269,77	^31	^1,874 x10^-4
^6	^3,0	^323,73	^38	^7,123 x10^-3

Do obliczenia wartości ładunku wykorzystano wzór q=b
gdzie

b- stała balistyczna

- wychylenie

Aby obliczyc siłe nacisku wykorzystano zależnośc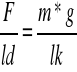

ld- ramie dłuższe = 110 cm

lk- ramię krótsze = 10 cm

m- masa obciążnika

g- przyspieszenie ziemskie = 9,81

Moduł piezoelektryczny wyznaczono z zależności
.Użyto w tym celu programu ORIGIN. Wykres tej zależności przedstawia linie prostą co pokazuje osiągnięty wykres siły [F] od ładunku [C]

Moduł piezoelektryczny wynosi 8,50575 x 10^-7 Błąd
= 2,08936 x 10^-6

^{β=0.99 k=4}

^{Współczynnik t-Studenta wynosi t= 4,60 wiec pomnożono bład}
ze współczynnikiem t

*t = 9,7 x 10^-6

Ostatecznie moduł d₃₃ = (8,5 ± 0,97) x 10^-7

^WNIOSKI

^{Obliczona stała balistyczna , moduł piezoelektryczny oraz błędy z pewnością wynikają z błędu odczytu z galwanometru.}

^{Jak już wcześniej wspomniano odczyt był trudny ponieważ wskaźnik na galwanometrze bardzo szybko się poruszał dlatego wiec przyjęto błąd odczytu plus/minus 3 działki.}

^{Doświadczenie pokazało ze stała balistyczna jest zależna liniowo od ładunku i wychylenia. Również zostało udowodnione, że moduł piezoelektryczny jest zależny liniowo od odkształcenia i naprężenia. W ogólnym przypadku moduły piezoelektryczne d tworzą tensor trzeciego rzędu
. Naprężenie T oraz odkształcenie S tworzą symetryczne tensory drugiego rzędu
oraz}

---