28039 rezonans0009

-55-

(3-34)

Po wstawieniu do równań (3.31) i (3.32) odpowiednio wartości (3.33) i (3.34) otrzymuje się:

22;

F₃(4l) = F₄(4_c) =

(3.35)

Po prostych przekształceniach można zauważyć, że Ęr = 1 jest średnią geometryczną Ę,i i Ęć-

4=VSfc⁼¹-    0.36)

Charakterystyki F₂(£), F₃(£), F₄(£) dla dobroci Q_sz-42 przedstawiono na rys. 3.9. Kształt tych krzywych zależy tylko od wartości dobroci obwodu rezonansowego.

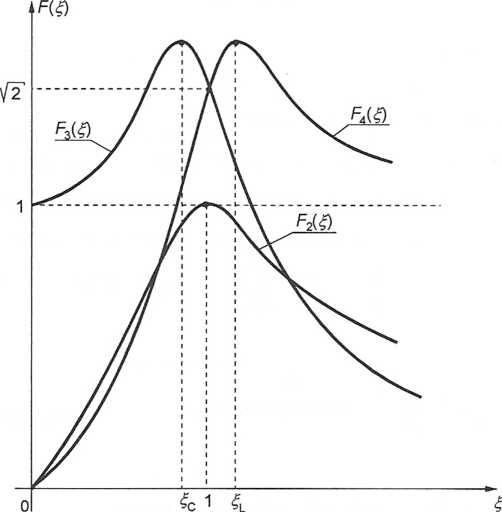
Rys. 3.9

Przy zasilaniu gałęzi szeregowej RLC z idealnego źródła prądu o stałej wartości skutecznej [7], charakterystyki częstotliwościowe opisane są zależnościami:

(3.37)

\U_l\ = coL\I\,

\I

^{1 c|} ć)C'