34111 str098 (5)

98 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

bo w przeciwnym razie punkt wewnętrzny z = 0 przeszedłby w punkt zewnętrzny w = oo. Wobec powyższego przekształcenie (1) możemy napisać w postaci

(2)

b

zH--

a a

w = —--.

d c —z + 1

Punktom z_t = -b/a, z₂ = —djc w płaszczyźnie (z) odpowiadają w płaszczyźnie (w) w myśl (2) odpowiednio punkty w,= 0, *v₂ =oo. Ponieważ punkty w₂ — 0 i w₂ = oo są symetryczne względem okręgu M = R₂, więc i punkty z_l = -b/a oraz z₂=-d/c muszą być symetryczne względem okręgu \z\ =R_t. Jeżeli więc

b

— = a,

a

(3)

to

w    c a

Uwzględniając związki (3) i (4) we wzorze (2), mamy

d R\

skąd

(9)

gdzie (p jest dowolną liczbą i Podstawiając równość (9)

(10)

Zauważmy na koniec, że puri jący mu punkt w = 0 leży w

(5)

a z—a ( a\ z—a

^{W =} ~d i " V ^7 5    "

~Ę^Z+1    r;*-¹

Aby wyznaczyć współczynnik    wykorzystujemy fakt, że punktowi z = R^e"

okręgu |z| = Ri odpowiada pewien punkt okręgu |w| = R₂. Wobec tego ze wzoru (5) otrzymujemy

a

= R

■2 9

ĄR^-l

R]

stąd po przekształceniach

(6)

lub

(7)

Ale

(8)

R,

R_ieⁱ⁰-a

cc e‘^e —Rj

= R,

R i

Pi-ae^-ie

R_L—<xe

-i0

— Ri + OLC

R₂- ae^w

Uwzględniając związki (8) we wzorze (7), mamy

Rz

\eⁱ⁰\ = R₂

Ri’

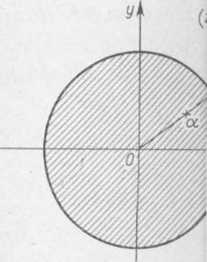
Reasumując stwierdzamy, a — dowolną liczbą zespolon (rys. 1.24). W szczególności I

(U)

gdzie (p jest dowolną liczbą i w koło jednostkowa |iv|<1 w t dek koła M<1.

Zadanie 11.4. Znaleźć fui o wierzchołkach z, = (3+2/), kątny i równoramienny sposób, że wierzchołki z* p (rys. 1.25).

Rozwiązanie. Z tego, że w trójkąt prostokątny i równ

(1)

Z warunków zadania wynika

(2)

7*