38270 str114 (5)

114 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Jt z

2) funkcja w = —ln— przekształca wycinek koła r<r₀ i 0< (/> < a₀ na płaszczyźnie «o r₀

z — x+iy = re^f,> w pasmo m^O i    na płaszczyźnie w = u+iv.

Rozwiązanie. Funkcje t(x,y) i t(u,v) opisujące rozważane tutaj stacjonarne pole temperatury spełniają równanie Laplace’a, są zatem funkcjami harmonicznymi. Dla znalezienia funkcji t(x,y) skorzystamy z danej funkcji w(z)

n x — iy

w(z') = u(x,y)+iv(x,y)=--ln-.

^ao r₀

Po oddzieleniu części rzeczywistej i części urojonej w funkcji w (z) możemy napisać

n> r₀    ,    . n ^!y

u(x,y) = —    «(*,jO = -arctg—.

\    za o x + y    <x₀ x    .

Jeżeli zmienną zespoloną z wyrazimy w postaci wykładniczej z = re^i,p, to funkcje u i v uzależniamy od współrzędnych biegunowych r i cp

, . n r₀    ^rn

u (r) = —ln —,    v(ę) = —ę.

a₀ r    a₀

Z powyższych zależności widać, że funkcja w (z) przekształca prostą = 0 w prostą v = 0, prostą <p = a₀ w prostą v — n oraz okrąg r = r₀ w prostą w = 0 (rys. 1.37).

Jeżeli otrzymane funkcje u(x,j) i v(x, y) wprowadzimy do danej zależności t(u,v), to otrzymamy szukaną funkcję t(x, y) opisującą pole temperatury w rozważanym pręcie o przekroju wycinka kołowego

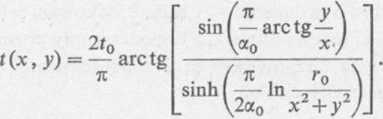
We współrzędnych biegunowych r, (p powyższa funkcja przyjmuje następującą postać:

„    ,    2I_{0 f}

t(r, <p) - — arctg n

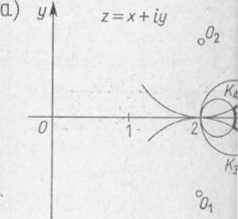
Zadanie 11.17. Wyznaczyć rozkład potencjału <p(x, y) w elektrycznym polu przepływowym wytworzonym w płacie folii metalowej, której obszar płaski jest ograniczony łukami okręgów

JC₁=(x-2)²+(y + l)²-l=0,

JC₂ = (x-2)²+(y-l)²-l = 0,

K₃ = (x-i)² + y²=±,

K_4S(x-f)² + y² = _TV

(patrz zakreskowany obszar na rys. 1.38a).

Punkty znajdujące się na leżące na okręgu K₃ mają pot kół Ki i K₂ są izolowane elektr Rozwiązać podane zagadn

przekształca rozważany obsza

Rozwiązanie. Na wstępie v = i, okrąg K₂ w prostą v = co widać po rozdzieleniu funk Mamy bowiem z = x+iy, za

w(z) = u-

Potencjał <p\it, v) pola przepły przez funkcję w (z) na szukan

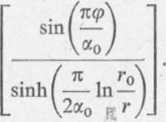
(p(3,v) =

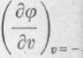
zatem <p(u,v) jest funkcją na<

Jeżeli do powyższej zależności danej funkcji iv(z), to otrzyma żanym płacie folii metalowej.

która po prostym przekształć

8*

4