39308 P1050620

Miejsca geometryczne pierwiastków

W-

Koniecznym i dostatecznym warunkiem stabilności układu jest, aby pierwiastki równani charakterystycznego układu zamkniętego miały ujemne części rzeczywiste

RJs_k)^<0.

Wówczas

gdzie: A - jest współczynnikiem o wartości skończonej i układ jest stabilny. Jeżeli chocia jeden z pierwiastków równania ma część rzeczywistą dodatnią

RJs_i)^>0,

wówczas

lim_l__ttey(t) = co

i układ jest niestabilny.

Jeżeli równanie posiada, chociaż jeden pierwiastek równy zeru, to układ jest niestabilny.

v

Kryterium Nyouista

Kryterium Nyquista posiada duże znaczenie praktyczne, ponieważ pozwala bada stabilność układu zamkniętego na podstawie przebiegu charakterystyki częstotliwościowi układu otwartego, którą można wyznaczyć zarówno analitycznie jak i doświadczalnie.

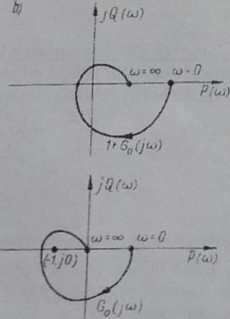
"Jeżeli otwarty układ automatyki jest stabilny i jego charakterystyka amplitudowo-fazow    ^R*^VŁ 7 Charakterystyki Grfaj: a - układów stabilnych, b - układów niestabilnych.

GoQaj dla pulsacji to od 0 do +co nie obejmuje punktu (-1, jO), to po zamknięciu bedzie o Logarytmiczne kryterium Nyąuista. Zapas stabilności

Rozważmy dwa układy otwarte, których charakterystyki amplitudowo-fazowe przedstawione są na rys. 8 Układ "a" będzie po zamknięciu stabilny, natomiast układ "b" niestabilny.

również stabilny" O)

pm

]QM

uj*Q

Pm

t7

t'6₀(jL>)

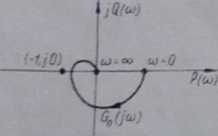
Rys. 8 Charakterystyki Gg(ja}: a - układ stabilny, b - układ niestabilny.

Dla prostych układów automatyki o charakterystykach częstotliwościowych typu przedstawionego na rys. 8 kryterium stabilności można sformułować:

Rys. 6 Układ zamknięty będzie; a - stabilny, b - niestabilny.

, "Zamknięty układ automatyki jest stabilny, jeżeli logarytmiczna charakterystyka amplitudowa / układu otwartego posiada wartość ujemną przy pulsacji odpowiadającej przesunięciu W przypadku złożonego kształtu krzywych GoQ(o) wygodnie jest posługiwać się wynikając fazowemu -I80°".

bezpośrednio z podanego kryterium tzw. regułą lewej strony", która mówi, że ukła fyj_a j-y_S 9 przedstawiono charakterystyki L(fó) i (p{(4 równoważne krzywym GoQa)) z rys. 8.

ętyjest stabilny, jeżeli punkt (-1, jO), znajduje się w obszarze leżącym po lewej stroni p_rosta konstrukcja graficzna pozwala nie tylko na sprawdzenie stabilności układu, lecz charakterystyki Go(jaj_t idąc w stronę rosnących o).    i również na liczbową ocenę tzw. zapasu stabilności. Zapas stabilności jest określony za

pomocą zapasu modułu AL (w decybelach) i zapasu fazy A<p (w stopniach lub radianach)