40972 MATEMATYKA062

116 111 Rachunek rótniczkowy

Zauważmy jeszcze, że lun f(x) = O = f(-1> i lim f(x) = l = f(0).

x—♦ U    x-*0-

Oznacza lo, że funkcja f jest prawostronnie ciągła w punkcie x, = - 1 oraz lewostronnie ciągła w punkcie x₂ =0.

PRZYKŁAD 2.1 Zbadamy ciągłość funkcji f w punkcie x₀ = l:

3x' +x² -4x

f(x) =

x-l

2.

xU x= 1

Z określenia funkcji f mamy f(l) - 2. Obliczamy granicę

_Ci v ,    3x³+x²-4x

lim f(x) = lim

X- vl    X >1

X — 1

= limx(3x+4) = 7

|0j X .i x -1

x-»l

Ponieważ lim f(x) * f(l), więc funkcja ta nie jest ciągła w punkcie x₀ =

x-*l

PRZYKŁAD 2.2 Zbadamy ciągłość funkcji

x+e \    x<0,

f(x) = < ln^:x

x>().

.3+ln~ x

Funkcja f jest ciągła dla x€(-x,0) oraz dla \€(0,-kc) jako funkcja elementarna. Pozostaje zbadać ciągłość tej funkcji w punkcie x = 0. Ponieważ

lim f(x) = lim (x + e )»1,

x-*0-    x*0-

lim f(x) = lim -¹'-■ r-x ><>♦    * *o* 3 + In ‘ \ i +°°

+oo

- lim

1

3

ln²x

+ 1

1,

więc lim f(x) lim f(x) limf(x)*l f(0).

X *0    x *0"    x *0-

Oznacza lo, że funkcja f jesl ciągła w punkcie x = 0. Tak więc, badana funkcja jest ciągła dla x e(-oo,+a>)    ■

f(x) =

PRZYKŁAD 2.3 Wykażemy, że dla funkcji Dinchleta *1 dla x wymiernych,

O dla x niewymiernych, określonej na zbiorze liczb rzeczywistych, każdy punkt dziedziny jest punktem nieciągłości (oczywiście jest to funkcja nicclementama).

Niech x₀ oznacza dowolnie ustaloną liczbę rzeczywistą (wymierną lub niewymierną). Oznaczmy przez (x*) dowolny ciąg liczb wymiernych zbieżny do x₀ oraz przez (x") dowolny ciąg liczb niewymiernych zbieżny do x₀. Wówczas

lim f(x^) = lim 1 = 1, lim f(x") = lim 0 — 0,

n-*»    n—*»>    n'>«o    n

co oznacza, że funkcja f nic ma granicy w punkcie x₀, a zatem nie jest ciągła w tym punkcie, Wobec dowolności punktu x₀ wykazaliśmy, że każdy punkt x € R jest punktem nieciągłości (drugiego rodzaju) funkc^f.

WŁASNOŚCI FUNKCJI CIĄGŁYCH. Omówimy teraz trzy ważne własności funkcji ciągłych: o lokalnym zachowaniu znaku, o przy jmowaniu wartości pośrednich oraz o osiąganiu wartości najmniejszej i największej.

WŁASNOŚĆ I (o lokalnym zachowaniu znaku). Jeżeli funkcja f jest ciągła w punkcie x₀ i ma w tym punkcie wartość dodatnią (ujemną), to przyjmuje wartości dodatnie (ujemne) w każdym punkcie pewnego otoczenia punktu x₀.

Zatem

( f jest ciągła w x_n i f(x₀)> 0)=> V A f(x)>0

U<x„l x<U(x»)

lub

( f jest ciągła w x₀ i f(x₀)<0)=> V A f(x)<0.

l/(x„> x<Ufx„)

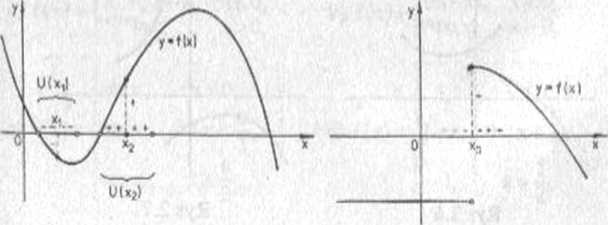
Rys 2.2

Rys 2.3