72960 str075 (2)

Ponieważ trójkąty ADO IDEO ponlndM|ą ińwim i t inwy (nlnln prędkość liniowo) I wspólny wierzchołek stwierdzimy, żo Ich polo »ą mililn luwim Nnlnmliint polo trójkątów DEO 1 ODG nn również sobie równe, joko polo figur o wr»|ióln«i| pinlrtlnwle (OD) I wierzchołkach G I E łożących na prostej równoległej do OD. Dochodzimy w Inn sposób do II prawa Keplera zauwa-żnjąo, że pola trójkątów ADO I ODG są soblti równo Uogólniając poczynione spostrzeżenie można stwierdzić, że promień wodzący satelity /określ, i podczas obiegu Ziemi wycinki po-wlorzchnl o równych polach w równych przedziałach czasu. Prawo to dotyczy tak zwanej prędkości pniowej satelity w jego ruchu wokół Ziemi.

Pi/odstawiając geometrycznie powierzchnię orbity sztucznego satelity Ziemi (rys. 6.8) driiglo prawo Keplera zapisać można jako

51 = 52 = 53.    (6.13)

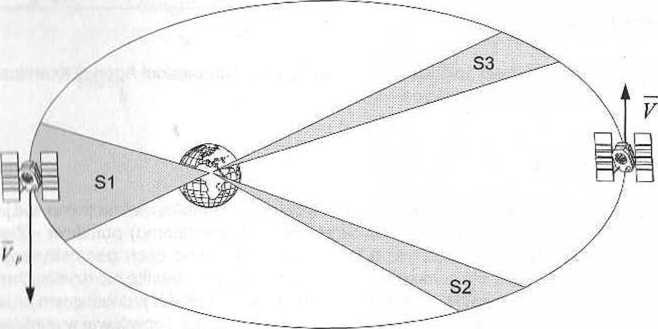
Rys. 6.8. Prędkość połowa satelity na orbicie.

W kolejnym prawie Kepler wykazał, że ruch satelity wokół ciała centralnego - Ziemi nie odbywa się w sposób jednostajny (stała prędkość liniowa). W apogeum jest on wolniejszy, n w pmygeum szybszy. W przypadku systemu GPS, którego orbita posiada małe spłaszczenie prędkości, te w rzeczywistości niewiele się różnią.

Zmiana prędkości liniowej w zależności od położenia satelity na orbicie odgrywa istotne /nai zonie przy projektowaniu systemu satelitarnego wynikającego z jego przeznaczenia. Na pi/ykłud orbity satelitów szpiegowskich są eliptyczne o dużej wartości mimośrodu. Podykto-w.u n> jest to koniecznością aby nad niektórymi punktami satelita poruszał się wolniej a nad Innymi szybciej.

Hi4

6.2.3.3. Trzodo prnwo

Trzecio z praw Kopiom podaje związek pomiędzy nknmom obiegu planety wokół Słońca a promieniem orbity. Przypomnijmy związek (0.7) pottlaol

(6.14)

GMm mV^!

oraz zauważmy, że prędkości liniowej V satelity odpowiada oczywista zależność

V

2nr

~T

(6.15)

gdzie:

T - okres obiegu satelity wokół ciała centralnego. Podstawiając prędkość z (6.15) do (6.14) otrzymamy

(6.10)

stąd

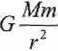
— m

4?tV² T²r

(6.17)

Po uporządkowaniu czynników otrzymamy postać III prawa Keplera

(6.18)

r³ GM T² ~4n² '

Dla wszystkich ciał niebieskich (sztucznych satelitów Ziemi) poruszających się wokół danego ciała centralnego o masie M stosunek trzeciej potęgi promienia do kwadratu okresu obiegu satelity jest stały. Gdyby rozważać ruch dwu ciał o masach m,, m₂ wokół ciała centralnego o masie M po orbitach eliptycznych, których półosie wynoszą a,, a₂ odpowiednio, to wygód nie jest posługiwać się III prawem Keplera w postaci ogólnej

Zj (M +    ) _ Q₁ ^    (6.19)

T²(M + m₂) a\

gdzie:

T_x,T₂ - są okresami obiegu ciał o masach m_x,m₂ wokół ciała centralnego.

Trzecie z praw Keplera odwołuje się do intuicyjnie oczywistej zasady mówiącej, iż, im większy jest promień orbity tym większy jest okres obiegu satelity. Związek pomiędzy promieniem i okresem orbity dla wybranych systemów satelitarnych zestawiono w tab. 6.4.

155