80492 str080 (5)

80 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Zi — 0. Poza tym jest wewnątrz tego konturu holomorficzna. Wobec tego zgodnie dzeniem o residuach mamy

-r    R    ♦

Ce^,xdx Ce^izdz    fe^lxdx    Ce^izdz

<3)    J—⁺ J — ⁺ J —⁺ J — - ²*'    •

z twier-

Wobec tego równość (5) pr

R

f sin

²ⁱ J-

r

c.

c_H

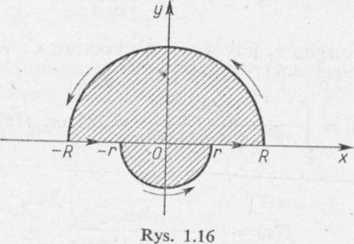
Wykażemy teraz, że druga całka celu rozwijamy funkcję podcalki wtedy

gdzie P(z), jako suma części w punkcie z — 0. Ponieważ prz jest ograniczona, to (10)

t

Biorąc pod uwagę, że równani

Zgodnie ze wzorem (10.2'), zastosowanym do funkcji f(z) z (2) w biegunie jednokrotnym Zy = 0, mamy

(4)    ,<*„/(*)

Uwzględniając wzór (4) w równości (3), mamy

.    f*

-r    R

f    e^udx |V’ił: te"dz

(5)    J—⁺J—⁺J—⁺J —“²”^M-

R    Cr    T    Cr

Podstawiając w pierwszej calce występującej po lewej stronie wzoru (5) x = —v, mamy fe^ixdx    f e~^ivdv    re~^!vdv Ce~^lvdv

⁽⁶⁾    J~'~J —"i —— J—■

-R    R    R    r

Zastępując w ostatniej całce po prawej stronie wzoru (6) v przez x, mamy

-r    R

f e^,xdx    f e~^lxdx

^<7)    J —“-J—•

— R    r

Biorąc pod uwagę równość (7), dodając pierwszą i trzecią całkę po lewej stronie wzoru (5) i uwzględniając wzór Eulera, otrzymujemy

R    R    R    R

re~‘^xdx    l'e^,xdx fe^,x—e~^tx ,    fsinjcd*

- J—⁺J—‘ J"²¹J—•

jo

gdzie    wyliczamy, że

oo    j

c

Całkując stronami wzór (9) p

(12)

*

c

Uwzględniając wzór (11) w r<

(13)

Przechodząc we wzorze (13) (

(14)

Wykażemy następnie, że trzeć R-+ co. Stosując wzór na całk nia z — Re¹¹, 0otrzym

6 — wybrane działy matematyki...