86482 MATEMATYKA031

54 I. Wiadomości wstyme
W szczególności definicje te zapisane dla funkcji rzeczywistej zmiennej rzeczywistej są dokładnie takie, jakie poznaliśmy w szkole średniej.
Uwaga Definiując granicę funkcji w punkcie p0 zakładaliśmy, te funkcja ta jest określona na pewnym sąsiedztwie punktu p0. Ogólniej (por Matematyka 2, rozdz II, 4) można rozważać granicę funkcji w takim punkcie put którego żadne sąsiedztwo nic zawiera się w dziedzinie D tej funkcji, ale istnieje przynajmniej jeden ciąg <p„) taki, że pn ei)-{p0} dla neN oraz pn—»p0. Taki punkt p„ nazywamy punktem skupienia zbioru D.
PRZYKŁAD 4 4
a) Obliczymy granicę funkcji f (x) =
w punkcie x0 = -2.
x2 -4
x + 2 r
Dziedziną tej funkcji jest zbiór D = (-oo,-2)u(-2,+oo). Niech (xn) oznacza dowolny ciąg o wyrazach należących do dowolnego sąsiedztwa punktu x0 = -2 i zbieżny do -2. Wówczas
= !im(xn -2) = -4.
lim f(xn) = lim
K-2)(x„+2)
x. +2
Zatem zgodnie z definicją Heinego granicy funkcji, mamy lim f(x) = -4.
X »-2
b) Obliczymy granicę funkcji dwóch zmiennych f(x,y) = —r—-
x‘ +y
w'punkcie p0 =(-1,2).
Dziedziną funkcji f jest zbiór D = R 3 - ((0,0)}. Niech ciąg punktów pn = (xn,yn) będzie dowolnym ciągiem o wyrazach nalezącycłi do dowolnego sąsiedztwa S(p0) c D. zbieżnym do p0. Ponieważ (Pn = (*n.y.)->H.2» <=> A y„-»2),
więc
2
5*
lim
n-*«e
f(p„)= lim f(x„,yn) = lim ^j- = -
«-►* n-»® x + y
Oznacza to, żc

<x,y) K-».2) X2 4 y 3
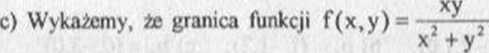
p0 = (0,0) nic istnieje.
Dziedziną tej funkcji jest zbiór D = R -{(0,0)}. Niech
P" = (n’n* oraz P" = <n,‘n^ dla n€N w>'raz>' ci^ów (PÓ) » (P«)
należą do sąsiedztwa punktu p0 i ciągi te są zbiezne do punktu p0 = (0,0). Natomiast granice ciągów (f(p')) i (f(p")) są różne
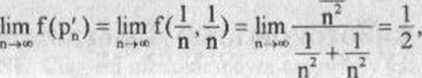
3
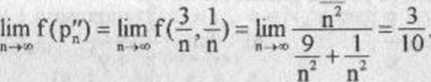
Oznacza to, że granica funkcji f w punkcie p0 nie istnieje.
W dalszym ciągu będziemy szczególnie dokładnie omawiać ciągi o wyrazach rzeczywistych, funkcje o wartościach rzeczywistych jednej i wielu zmiennych, a granica będzie jednym z podstawowych pojęć rozważanych przy tej okazji. Warto zdawać sobie sprawę z tego, że określenia granic, które wiedy będziemy formułować będą stanowiły szczególny przypadek definicji podanych w tym paragrafie
ZADANIA DO ROZWIĄZANIA
l. Obliczyć granice ciągu (pn), gdy:
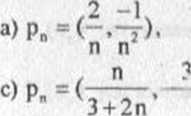
b) pft = (5-\l+3"-V)
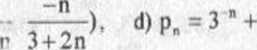
Wyszukiwarka
Podobne podstrony:
MATEMATYKA014 20 I Wiadomości wstyme Ponieważ -16= 16(costc + i sin rc), więc. zgodnie z (2.8), mamy
skanuj0030 (6) Vl.1 Określenie funkcji wielu zmiennych 211 . Z podanej definicji w
skanuj0031 (6) VI. 1. Określenie funkcji wielu imiennych 211 Z podanej definicji w
stat PageG resize 47 Statystyka matematyczna Testy zgodności z rozkładem normalnym Testy te sprawdz
IMGQ83 Mechanika Płynów - wykład I - s.l 1. Wiadomości wstępne. Podstawowe definic
page0440 438 PLATOM. w każdej rzeczy przedewszystkiem jej istoty należycie określonej, a definicyę t
MATEMATYKA013 18 I Wiadomoicl wstępne 18 I Wiadomoicl wstępne i zapisujemy Zatem (2.7) = Vw. der (z
MATEMATYKA018 28 I. Wiadomości wstąptt* funkcji f jest zbiór liczb rzeczywistych y£l, czyli przedzia
MATEMATYKA019 30 L Wiadomości wstępne Zatem funkcje f,(x) = l-x2, xgR, oraz f2(x) = l-x2, xeR nie są
więcej podobnych podstron