223 (58)

346

co podstawione do (IX.9) daje

(IX. 12)

Uwzględniając (IX. 12) we wzorze (IX.2) otrzymujemy wzór na współczynnik samoprzegrzania

IHHgjj B

pozwalający obliczyć wartość /, jeżeli znamy parametry obiegu T₀, T₂, sprawność wewnętrzną turbiny oraz liczbę jej stopni z:

/-/(to. ti.ą^.z).

Przypomnijmy, że relacja (IX. 13) została wyprowadzona dla szczególnego przypadku, gdy cała ekspansja odbywa się w obszarze pary mokrej, linia ekspansji jest przyjęta jako linia prosta, a spadki temperatury w stopniach są jednakowe.

Wzorem tym można posługiwać się w przypadku turbin siłowni nuklearnych łekkowodnych, nie obowiązuje on w przypadku turbiny konwencjonalnej, gdy większa część ekspansji przebiega w obszarze pary przegrzanej.

W celu przybliżonej oceny współczynnika samoprzegrzania można skorzystać z półempirycznego wzoru Flugla [8]. który występujący w relacji (IX. 13) wyraz

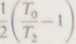
zastępuje wyrazem

k-H,.

Wzór (IX. 13) napiszemy więc w postaci:

(IX.14)

f — kH_a{ 1 — ;/_iT)— ---

Współczynnik k dla turbin (lub grupy stopni) pracujących tylko w obszarze pary przegrzanej (np. turbina WP siłowni z przegrzewem międzystopniowym) wynosi

0,48 “ 1000’

jeżeli linia ekspansji leży w obszarze pary mokrej

IpŁ

1000

wreszcie dla turbin, w których linia ekspansji zaczyna się w obszarze pary przegrzanej, a kończy poniżej krzywej granicznej x = 1

0,33+0,43

1000

We wzorze (IX. 14) należy podstawić H, w kJ/kg.

/ = *11,(1 -IfoJ “ = |jj|‘ 1000(1 -0,8)

2>. = (1 +/)H, - 1,072-1000 - 1072 kJ/kg.

Sprawność wewnętrzna turbiny jest w tym przykładzie 1,072 razy większa od średniej sprawności jej oddzielnych stopni.

W przypadku turbin gazowych, a także dla grup stopni pracujących w obszarze pary przegrzanej, można obliczyć analitycznie współczynnik samoprzegrzania, korzystając z równań obowiązujących dla gazu doskonałego.

Załóżmy, że proces ekspansji odbywa się w turbinie posiadającej nieskończenie wielką liczbę stopni, zaś wykładnik politropy

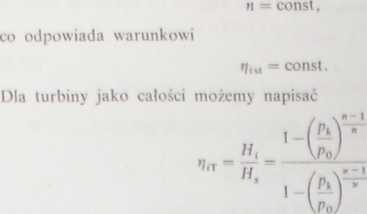
dla stopnia odpowiednio

n- 1

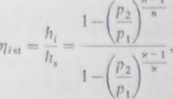
gdzie: p₀, p_k — ciśnienie przed i za turbiną (grupą stopni), p,, p₂ — ciśnienie przed i za dowolnym stopniem.