260 (31)

- 260 -

- 261

Rozwiązanie liniowego niejednorodnego równania różniczkowego (1) warunkami początkowymi (la) możemy otrzymać jako sumę rozwią_ZaD^_a

'•taj

w.

nia jednorodnego (całka ogólna) u^(t) i rozwiązania szczególnego _u" °*^tla' Równanie charakterystyczne równania różniczkowego (1) ma postać ^C

LCs^ + RCs +1=0.

Łatwo można stwierdzić, że pierwiastki równania charakterystycznego

ujemne i wobec tego w stanie ustalonym u'_c(t) = 0. Zatem napi=e-t_ . . ³'< stanie ustalonym będzie równe u"(t). Zgodnie z zadaniem 3.1

napięcie u_ (t)

,_s»t>i^eS y>i^>aie

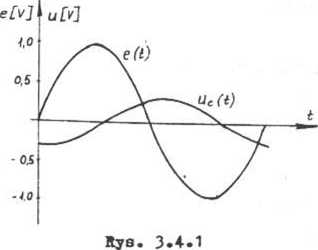
napięć e(t) i u_c(t) przedstawia rys. 3.4.1.

również rozwiązać, stosując metodę symboliczną.Wartość Bym

soli¹

eta®

^jjgymalna napięcia u_c(t) będzie równa

1 e

JO

R + j (tuL -

T

cud

.) 3^1

żyć, że napięcie u"(t) ma postać

można

0.316 e^¹⁰⁸⁰²⁴','

^uć'(t)

U_cmsin(2t + ę>_u),

U)

(4)

Rozwiązując układ rónnan ^ niemy

^Ucm “ -°.316 V    = 71

gdzie U i <f_n są tak dobrane, aby równanie (1) było spełnione. p_0lj. stawiając (2) do (1) otrzymamy

-U_cn^{sinl2t +} ?_u) ⁺ 3Ucm^{C0Sk2t +} ^ = ^sin2t*    (3)

Dokonując przekształceń trygonometrycznych, możemy (3) przedstawić w postaci

'-^!Jcm^cosr_u “ 3U_cmsin^_u)sin2t + (3U_cmcosę>_u - U^sini^)

cos2t = sin2t, a stąd:

^cn⁰⁰³^ = ^Ucm^sin^«

-^Ucm^cos^u - ^3Ucm^sin^ ^{= 1<} (4)

>36

czyli

u (t) =» -0,316 ain(2t + 71°360 =■ 0,316 ain(2t - 108°24')

i we⁰

u_c(t) = 0,316 sin(2t - 108°24') V.

Zadanie 3.5 id a)

x(t) = -p sin(2t - 15°).

V2

id b)

x(t) = —sin2t.

6^2

Zadanie l.fi

Możliwe najprostsze realizacje obwodowe równania różniczkowego a) z ^s<il 3.5 przedstawia rys. 3-6, a równanie b) rys. 3.6.1.

Rys. 3.6

(5)