266 (45)

METODY NUMERYCZNE.

Powyższe uporządkowania a, są wzięte z książki [95]. Tam też można znaleźć uporządkowanie a_t dla dowolnego m.

Przykład 10.10

Przedstawioną metodę Czebyszewa wykorzystamy do rozwiązania zadania różnicowego

(10.138)

x)=f„(x)_t    xeQ_h

W*) - <Ph(.x) ,    xeT_h gdzie

2

U u_h(x) = -0.5 JT (d£a_i}(x)Cj u_h(x))+ói(a_tj(x) d_i tf*(x)))+c(x) u_b(x)

Jest to zadanie różnicowe (10.15) — (10.16) zp. 10.2.3. Aproksymuje ono zagadnienie (10.12)—(10.13) dla ogólnego równania eliptycznego drugiego rzędu bez pochodnych pierwszego rzędu (ó, = 0, / = I, 2), rozważane w dowolnym ograniczonym obszarze Cl na płaszczyźnie. Przyjmując odpowiednie założenia

0    współczynnikach a_IJt c i rozwiązaniu w, udowodniliśmy w p. 10.2.6 stabilność

1    zbieżność zadania (10.138) (zob. twierdzenia 10.12 i 10.13).

W punkcie 10.2.6 zadanie (10.138) zapisaliśmy jako równanie operatorowe (zob. (10.41))

(10.139)

u* — fh

w przestrzeni L\ (Cl/,). Z lematu 10.1 i twierdzenia 10.11 wynika samosprzężoność i dodatniość operatora A_k.

Równanie (10.139) rozwiązujemy metodą (10.133). Jaki operator należy wziąć za 5? Rozpatrzymy najpierw przypadek, gdy B = E, czyli B jest operatorem tożsamościowym.

Sprawdzamy założenia opisane w (10.134).

Lemat 10.12

Jeśli u,₂ = a₂1, c (x) > 0 oraz istnieją stale dodatnie y₀ y, takie, żc dla dowolnych x e Q. £ = [<fi, Ć2]⁷ e R^z, £    0, zachodzi

22    2

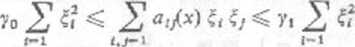
(10.140)

to

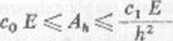
(10.141)

gdzie 1 = O, 1 są stałymi dodatnimi, które nic zależą od kroków /^siatki, lecz

jedynie od y, (odpowiednio) i średnicy obszaru Q, h = min {A_lt h₂}.