323 2

323

8.1. Podstawy teoretyczne

J&YAłaźyrny- funkcje ę>, są różniczkowalne względem a i rjj {«./=!• 2, ... s) dla kaź-_efab) • dia każdego punktu y z pewnego obszaru D. w którego wnętrzu leży r. ^⁰ j_ręoznikach równań różniczkowych - zob. np [100] - dowodzi się, żc przy łych. Bgggjgęh-zagadnienie początkowe (8.1.2) ma dokładnie jedno rozwiązanie (dopóki y (a) = _fnaczej mówiąc, ruch cząsteczki w danym polu prędkości jest jednoznacznie określony BBpIf^oJoźicnie początkowe. Dopóki cząsteczka pozostaje w obszarze, w którym, są Lcłaicne założenia o regularności (zob. przykład 8.1.2), prawdziwość tego twierdzenia ^daje się wynikać w oczywisty sposób z rys. 8.1.1; Tystmck sugeruje też. żc jeśli wybiera _się dostatecznie krótkie przedziały czasu, to zasada ,,przesunięcie=przyrost czasu x xśrcd»ia prędkość” pozwala budować krok po kroku rozwiązanie przybliżone. Jest to podstawowy pomysł większości metod całkowania numerycznego równań, różniczkowych.

IO.łI

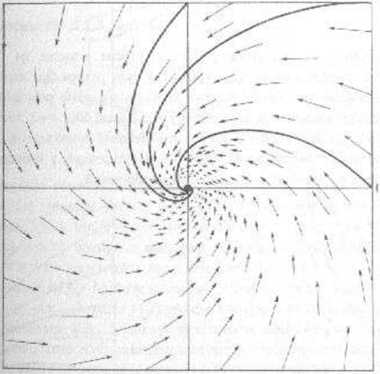
Rys. 8.1.1

U,i)

^^r^²*^CJ ^wy^&2ukanc konstrukcje ..średniej prędkości" w rozpatrywanym pt/c-^dai^,'ł różne metody rozważane w następnych paragrafach. Określa sie niekiedy ^S °d> jako symulacją dynamiczną iuh ciągłą układu.

■|P&KIao 8.1.3. Zagadnienie początkowe

“=y²,    ,v(0)= l

^    flX

ńJC2_ńS^^Cf^n,e >' (*) = 1/(1 - A). Zauważmy, że >1» - co, gdy x — !. Dlatego rozwśąza-^V&n,a istnieje tylko dla a* < J. n»