34 (230)

1. Pochodną funkcji skalarnej fPO względem wektora X jest (pochodna ta jest niekiedy zapisywana jako 3^ )

d/(X) j a/(X) a/(X)    d/(X)]

3X [    ' rlt₂    ax_m j

Wyrażenie

a/(X)

dX

-grud /(X) jest gradientem funkcji /(X).

2. Pochodną

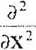
funkcji wektorowej F(X) względem wektora X jest macierz

3F(X) _ " dX ' ~	dX ~ a/2(X) dx		<)XJ d/2(Xj	3/i(X) rU'2 fj.Vj	a/ux) ‘ ^A'm ę>hm
	df„(X)			°fn(X>	%(X>
	r)X			(JXy	J

nazywana macierzą Jakobiego.

3²

—.....-sr ) jest macierz

3. Drugą pochodną “y funkcji /(X) (zapisywaną także jakc

d²/(X) _ 3 p/(X)" 3X²    3x[ 3X⁷ .

3^2/(X)	a^2/(X)	r)^2/<X)
	i5.r]ć) v2
?^2/(X)	r)^2/(X)	E ^ 3
		xm
<>V(X)	3^2/<X)	a^2/<x)
		3^

f. Niech /(B) będzie funkcją skalarną zmiennej macierzowej    Po

chodną /(B) funkcji względem macierzy B jest

		o^2
a)	- ----- AX = A,	AX = 0.
	0X	ax^2
b)	----- X^7 A Y = Y ^7 A^7 ,	----- X^7'A Y = 0,
	0X	> ox^2
c)	- X^7X — 2X'\	O^2 T ----- X^7X“2I,
	0X	0X^2
d)	— - X^7AX = X^7 (A^7 + A),	X^rAX = (fi
	ox	ox^2
el	---- • X^7 AX - 2X^7 A,	i^2 ----- X^7 AX = 2-
	ox	0X^2
		symetryczną),

A),

(gdy A jest macierzą

0 — Y^rBZ = YZ^r,

g)    A B C ~ A ®C⁷ ,

OB

h)    -Ł B = I.

OB

j) JLx⁷B X- ^xx'’ ^ ⁿ’^c j^{csl niac}’^erz4 symetryczna,

^    [2 X X⁷ - Diag(XX)^r, gdy B jest macierzą symetryczną,

q _ IC⁷ , gdy B nie jest macierzą symetryczną, dB    [C + C⁷ - Diag(C), gdy B jest macierzą symetryczną,

k) - Tr(B C B I)) = OB

T⁷ , gdy B nie jest macierzą symetryczną,

T + T - Diag(T), gdy B jest macierzą symetryczną, gdzie T ~ DBC + CBO.

Szereg Taylora

Niech /(X) =/(a-[,będzie funkcją skalarną różniczkowalną względem wszystkich elementów wektora X = [a_],X2,...,a„]^/ - Jeśli jest znana wartość tej funkcji w punkcie X° ={a[\at.....a^,}⁷ , to

dv+-d'J	V/(X)	]
X,x<> 2 *	ox^2	x=x° j

|d x ■+■ k

(1.43)

35