365 2

365

8.5. Równania różnicowe

W określonym tu sensie nawet metoda punktu środkowego zbadana w przykładach g. § 5.9 jest stabilna, ale jej niekorzystne własności ujawnione w pierwszym przykładzie ⁸ sadniają nazwę ,^netoda słabo stabilna(' (lub „słabo niestabilna").

^Otrafności określonego wyżej pojęcia stabilności świadczy poniższe twierdzenie łą-ę^ce w sobie kilka twierdzeń Henriciego ([110], rozdział 5). (Wskazówki do dowodu są zawarte w zadaniach 5 i 6(c) do tego paragrafu).

TWiERDZENic 8.5.4. Załóżmy, że y(x) Jest (p- iykrotnie różniczkowalnym rozwiązaniem zagadnienia początkowego (8.5.1 IX że ||/'^+l>(x)||<ję₎, p>\ i że funkcja f jest różniczkowana dla każdego y. Załóżmy też, że ciąg {y„}jest określony za pomocą związków

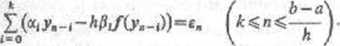
Jeśli metoda wielokrokowa jest Stabilna i spełnia warunek (8.5.13), to istnieją stale K_tt Kz, k_Q takie. że dla każdego x_u e [a. b] i każdego h^h₀ zachodzi nierówność

(8.5.15)    ||k,-J<*J||<(<*'(*.-«)Ko+

1*0

Stała K_y zależy tylko od współczynników metody, natomiast K₂ zależy także od oszacowania z góry normy ||/'(*)||.

Wobec tego wyniku liczbę całkowitą p nazywa się rzędem dokładności metody.

Aby wykazać, że stabilność i zgodność są konieczne dla tego wyniku z p>0, wystarczy rozważyć trywialny przypadek / (y)=const. Wnioskiem z twierdzenia i tej uwagi (w bardziej precyzyjnym sformułowaniu) jest to, że

(8.5.16)    zgodność a stabilnośćozbieżność.

Zbieżność oznacza tu zbieżność jednostajną w [a, b], gdy h -* 0, dla wszystkich funkcji /spełniających założenia z § 8.1.1, a także żądanie, aby skutek zaburzeń wartości początkowych dążył do zera, gdy same zaburzenia dążą do zera. Sformułowanie (8.5.16) występuje ^{w w,e}*^u innych zastosowaniach metod różnicowych do równań różniczkowych zwyczaj-®ych i cząstkowych, przy czym trzy pojęcia z (8.5.16) określa się stosownie do klasy za-„Zgodność” oznacza zwykle, żc równanie różnicowe jest zbieżne formalnie do równa-^{n,a r}&bttCfckowego_t gdy h -* 0, natomiast „zbieżność” jest związana z zachowaniem się ^r°7.w*iąza6 równań różnicowych.

$>9*0, to metoda jest niejawna; zob. § 8.3.4. Wtedy na ogół w każdym kroku trzeba ^zać ileracyjnie pewien układ nieliniowy. Jeśli koniec iteracji zależy' od wielkości >i to z ostatniego twierdzenia można otrzymać oszacowanie błędu. Jeśli stosuje się |^^*cę^ekstrapolacyjno-interpolacyjną z ustaloną liczbą iteracji, to wspomniane twier-ii- u    rosnąć. Typ stabilności takiego algorytmu może