370 2

370

8. Równania różniczkowe

12.    Obszar stabilności metody Rungego-Kutty (8.3.6) pokazano na rys. 8.5.2. Zrai** punkty przecięcia granicy obszaru z osią rzeczywistą i z osią urojoną (te ostatnie można otrzymać, rozwiązując zadanie 7 z § 8.3).

13.    Dla jakich dodatnich długości kroku h metoda Cowella zastosowana do równani różniczkowego

/'+*- o

daje rozwiązania ograniczone?

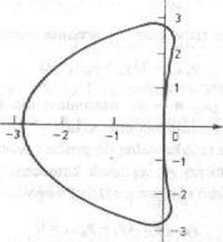
Rys. B.5.2

14.    Wykazać, źe metoda wsteczna rzędu drugiego określona równością

ry.+łr^!y.-hf(yj

jest stabilna typu .4(0). (W istocie jest ona stabilna typu A.)

15.    (a) Pokazać, że można określić i fJ₂ tak, aby dla metody wielokrokowej

y„” -4^,-1+5y.-a + h(fij(y_m„_s)+fiJiy_n-₂))

było p=3. Wyznaczyć stałą błędu c z (8.5.13).

(b) Tę metodę zastosowano dla h = 0.1 do zadania y'=y, j(0) = l, przy czym y\ było równe exp (0.1) z dokładnością do sześciu cyfr ułamkowych i tej samej dokładności używano w obliczeniach. Wartość y_XQ okazała się ujemna! Wyjaśnić, dlaczego powstał tak wielki błąd.

16.    Rozważyć przykład 8.5.8. Wyznaczyć skutki wygładzania według wzoru (8.3.3) dla qm — \_l A =*0.1, A'=I0.

17.    Zastosować metodę liniową wiełokrokową, określoną za pomocą wielomian^ p i er, do zwykłego zadania testowego y' = qy, y{0)= 1.

(a) Pokazać, że jeśli Cj jest zerem (pojedynczym) wielomianu p, to równanie różnico^® ma rozwiązanie szczególne równe w przy bliżeniu

y*= C / txp(XjqxJ    nk).