332 2

332

8. Równania różniczkowe

8.3. Inne metody rozwiązywania zagadnień początkowy dla równań różniczkowych zwyczajnymi

Metoda Eulera wraz z ekstrapolacja iterowaną Richardsona jest prosta w użyciu i w pewnych zastosowaniach - dostatecznie oszczędna. Rozwiązywanie zagadnień początkowych powoduje często bardzo długie obliczenia, wobec czego ich koszt jest istotną charakterystyką metody. Jest więc naturalne, że rozważa się i inne możliwe aspekty atakowania zagadnień początkowych.

8.3.1. Zmodyfikowana metoda punktu środkowego

Jeden ze sposobów opiera się na lepszym wzorze różniczkowania numerycznego, tj. wzorze symetrycznym

jp(x_J,-,>-.v(x_łł.₁)    .

y(x_n)=--—    +0(h ).

2/i

Otrzymuje się stąd wzór rekurencyjny określający jawną metodę punktu środkowego:

(8-3.1)    y_n< i-*-.+2V<»«r3k).

Jest to metoda dwukrokowa, gdyż wartość >•„_ _t wyraża się w niej przez dwie poprzednie, mianowicie y„. , i y„ (por. pojęcie metody jednokrokowej określone w $ 8.1.2). Wymaga to specjalnego wzoru służącego do obliczania y,. Lokalny błąd obcięcia w (8.3.1) jest rzędu 0(ń³); wobec tego błąd globalny wynosi 0{h²). Poniższy przykład świadczy o tym, że nie jest to metoda dostatecznie ogólna.

Przykład 8.3.1. Zastosujmy wzór (8.3.1) do równania y' — —y, y(0)= 1. Przyjmijmy A=0.1, v₀=l. Rozwiązanie otrzymane dla y, =0.9 oznaczono na rys. 8.3.1 czarnymi kółkami, a rozwiązanie odpowiadające wartości >^=>0.85 kółkami niczaczcmionymi.

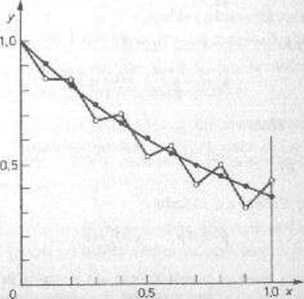
Rys S.3.1