337 2

337

8.3. Inne metody rozwiązywania zagadnień początkowych

z tym przypału. i^ak ‘ 'ⁿⁿ>^c^ funkcji f błąd globalny obcięcia jest równy

^ Istnieje wiele metod Rungego-Kutty o różnych zaletach. Można np. osiągnąć dokład-rzędu piątego, obliczając sześciokrotnie funkcję / w jednym kroku. Systematyczne

83.4. Metody niejawne

Metoda trapezów opisana wzorem

(8.37)    i-^^BP [/(^ * y*)+/(^x»n. y.+i>] (n«0,1,...)

jest przykładem metody niejawnej, gdyż przybliżenie y_K+t, które należy obliczyć (w n-tym kroku) występuje również po prawej stronie wzoru. Jeśli /jest funkcją nieliniową względem v, to w każdym kroku trzeba rozwiązać układ nieliniowy. Trzeba to zrobić jakąś metodą iteracyjną - np. za pomocą procedury

(8.3.8)

gdzie u_M=y_K+łkf(x_a, y„) jest znane z poprzedniego kroku. Zgodnie z (6.9.3) warunkiem wystarczającym zbieżności jest nierówność

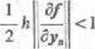
i ;m mniejsza jest jej lewa strona, tym zbieżność jest szybsza. Zupełnie dobre przybliżenie początkowe można otrzymać z poprzednich wartości, np. za pcmocą wzoru

yiVi=y_ą+kf(x„,y₀).

Taki wzór nazywa się zwykle wzorem wstępnym, natomiast wzór niejawny z (8.3.7) — wzorem korygującym. Cafe postępowanie określa się też jako metodę eksirapoiacyjno-inier-peiacyjną. Koniec iteracji wyznacza się albo porównując różnicę jrjJjY*—ji*+i z pewną zadaną tolerancją e, albo ustalając z góry liczbę iteracji. Częściej stosuje się to drugie rozwijpanie. Jeśli np. decydujemy się poprzestawać zawsze na obliczeniu v£Vi, to otrzymujemy znów metodę Hcuna (8.3.4). Jest ważne, aby wybrać taki wzór wstępny, żeby jedna iteracja dawała niemal pełną dokładność tego, co powinno się otrzymać z wzoru korygującego.

Klasyczny schemat ckstrapolacyjno-interpolacyjny jest opisany poniższymi wzorami, ^w których /.=/(jc„, a P jest operatorem różnicy wstecznej.

Wzór Adamsa-Bask for tka: