405 2

9.4. Przedłużanie okresowe funkcji nieokresowej

405

pjujyjecCTą nierówność można stosunkowo łatwo sprawdzić, korzystając z (9.2.3) ) . . jy^rotnego różniczkowania przez części).

'' Niekiedy szeregi Fouriera stosuje się do funkcji określonych tylko w przedziale (-*, *). definiuje wtedy przedłużenie okresowe funkcji poza ten przedział (rys. 9.4.1).

v-~v-

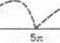
Rys. 9.4.1

Określenie jest więc takie, żc /(*)=/(*+2it) dla każdego X Przy tej metodzie mogą wystąpi nieciągłości funkcji lub jej pochodnych dla x*=n. Powodują one wolną zbieżność szeregu nawet wtedy, gdy funkcja jest bardzo regularna w przedziale (-ic, it). Istnieją i inne sposoby przedłużenia funkcji poza przedział, w którym była pierwotnie określona. Jeśli funkcja jest zdefiniowana w [0, it] i jeśli/(0)=/(tc)=0, to można przedłuźyć/na przedział f-rc, 0], przyjmując, że/(*)=-/(-*)■ Następnie przedłuża się funkcję okresowo

Rys. 9.4.2

(poza przedział [-ti, tc]) wzorem f(x)=f(x±2x) (zob. rys. 9.4.2). Ponieważ otrzymana funkcja jest nieparzysta, więc jej szereg Fouriera zawiera tylko sinusy (zob. twierdzenia 9.Z3 i 9.2.4).

Przypadek ciągły:

(9A2)    £ bjsmjx,

J-1

Przypadek dyskretny:

(9.4 3) gdzie

41

gdzie ó^=— I f(x) sin jxdx.

Y bj*injx,

i-i

jra

N +1 '

takiego rozwinięcia sinusowego można skorzystać nawet wtedy, gdy/(0)^0 lub/(*)^0, ^{c w}    przypadkach jest ono wolno zbieżne.

. ^podobny sposób można przedłużać funkcję tak, aby powstała funkcja była okresowa P^&r2ysta (rys, 9.4.3), Jęj szereg Fouriera zawiera więc tylko cosinusy.

— t.    0    n    2re

Rys. 9.4.3