43 (277)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA 173

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA 173

(* + l)² ’ (*+l)² ’ U + lr’ (Jt+l)^a

248. —5—. ^Sk

lilii’ ’ li l.ll- " li lii* ' /i-tli

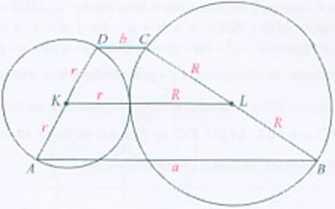
Rozwiązanie. Wykażemy, Ze sumy długości przeciwległych boków trapezu są równe, czyli, ze u + /> - 2r + 2K.

Odcinek KI. jest odcinkiem łączącym środki ramion trapezu. więc jego długość jest równ;i połowie sumy długości podstaw trapezu. Zatem | KL\=r + K = 0.5(<r + In Stąd d + /» = 2r + 2A\

252. \zK I = 70*. | ZL | = 130^c. | ZMI = 110°. IZS |=50°.    ^--

Wskazówki. I. Przekątne czwoiok.it.i KLMS mi prostopadłe do odpowiednich jego boków. II..Skorzystaj z równości między odpowiednimi katami wpisanymi i kipami między styczną a cięciwami okręgu.

253.    IZA 1 = 50°. | ZII| = 'X)°. |ZC\~W. \ ZD\ = 130”.

Rozwiązanie. Kąty ABC i ADC są kątami wpisanymi w okrąg opartymi na średnicy, więc są kątami prostymi. Kąl BAD jest kątem wpisanym, opartym na tym samym, co kąt środkowy BSD, więc I ZBAD I =0.5-1 ZBSD\ - 50°. Suma miar kątów czworokąta wynosi 3h0^o, zatem ZbCD\ =360'^,-(50^o+9n^#+y0^oj = l30^o.

254.    70”. 8t>°. 100°. 110”.

Wskazówka. Skorzystaj z. równości kątów wpisanych opartych na tym samym luku.

256.    IZ.4I = 40°. IZM=70\ I^Z>I= 110°. \ZO= 140°.

Rozwiązanie. DBC jest trójkątem równoramiennym o kącie pr/y podstawie 2l)“. więc ZBCD | = 141) . Kąi ADB jest prosty (jest kątem opartym na średnicy), więc | ZADC I = 90“ + 20“ = 110⁸.

Korzystając z tw. o czworokącie wpisanym w oirąj,\ znajdujemy I ZltAC I =40° i I ZABC | = 70“.

257.    60",80“. KXr\l2tr.    258. IZflł-60”. IZC1= 100°. IZZ)ł= 120”.

263. 1^1*60°.

Rozwiązani*. Ozn. a - miata kąta BAC.    \ ZABC \ + \ ZACB \ = 1 80° - ot.

\ZOBC\ + \ ZBCO\ - 0.5 ( | ZABC\ +1 ZACBI) = 0.5(180°-«) = 'H)”-0.5rz    \ ZTOS\ = \zCOB\ - 180°-(W 0.5rt) = ÓU“+0.5tt

Na czworokącie ATOS można opisać okrąg, więc \ZTOS I t! ZTAS \ - 180°. Zatem ')<• + D.5rr+ ti= 180’. stąd n =60°.

265. Sześć razy.

|A'5'| “ = a 2a = 8bVh. Stąd a = 6b.

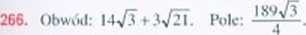
Rozwiązanie, a - długość boku AB. /> - długość boku CL). Gdybyśmy poprowadzili prostą przechodzącą przez punkt K. która fest styczną w punkcie 5 do okręgu opisanego na czworokącie ABCIK to na mocy iw. o związkach miarowych między odcinkami stycznej i siecznej

Wskazówka. Uzasadnij, ze trójkąt ABC jest równoboczny. Wykorzystując równość kątów ADB i BDC, uzasadnij, ze \AD\=2\DC\.

H

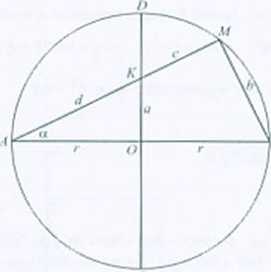
267. \ZBAM\ -■ 30°.

Rozwiązanie. ZAMB jest oparty na średnicy, więc \ZAMB\ = 90³. O -^-=sinrz. 0 =cos<z, © y=tgn'. O -C = cos a. W czworokąt OBM K rno/na wpisać okrąg, więc © <i t h - e * r. Wyznaczając z równości O ©, ©. O a, b. c i pod

stawiając do równości W. otrzymujemy rtgrr + 2/sinz/ = 2rco»« —— ^ + r. Dzieląc obie strony tego równania przez r otrzymujemy równanie trygonometryez-

stawiając do równości ©. otrzymujemy rtgrr + 2/sinz/ = 2rco»«    —-—• + r.

Stąd juZ. lalwo uzasadnić. Ze sinzr= 0.5. czyli a-30”.

Uwaga. Otrzymane równanie trygonometryczne można rozwiązai w prostszy sposób korzystąjąt ze wzorów na funkcje trygonometryczne podwojonego kąta i wzorów na sumy funkcji trygonometrycznych, których znajomość nie jest wymagana na maturze.