9 (971)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA 139

2.43 21.

Rozwiązanie. Kąt ostry równolcgłoboku ma miarę ISO'- 15(f" = 3ft°. Pole równoleglobnku: /'=(i- 7 sin.3l)^J = 2l.

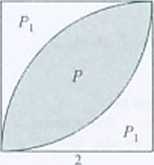
2.44 2*-4.

Rozwiązanie. Pole kwadratu 5=4.    P=S-2P,, P_t=S- -jfr-2² =S-fT.

Ziłem P=S-2-(S-/t)=2/r-S=2a-4.

2.45 A(P. 65°. 75°.

Rozwiązanie. Miara kąta wpisanego jest równa połowie miary kąta .środkowego opartego na tym samym luku, więc IZACB\ = \ IZASBI i

WAa*\\ ZBSC\^65>. \ZABO = 180*- ('40®+65°)=75°.

2.46 4(P. 60°. 80".

Wskazówka. Stosunek miar kątów środkowych opartych na wyznaczonych lukach wynosi 2 : 3:4. Suma tych kątów środkowych jest kątem pełnym.

| ZBCA | = 46° i | ZCAB\ = 54“.

r:

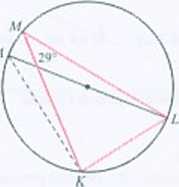
2.47 29*. 61°. 9(1°.

Rozwiązanie. Kąty KML i KM. są kątami wpisanymi opartymi na tym samym luku. więc mają równe miaiy. Zatem | ZAVW. | = 2‘/\ Kąt A KI. jest kątem wpisanym opartym na średnicy, więc jrslkątem prostym. | ZKLA i = 180°-(29°+90") = 61°.

2.48 iZ/tBf| = SD°. \ZHCA |=4f*°. |zCAfl| = 54°.

Rozwiązaniu. Odpowiednie kąty wpisane i kąty między styczną a cięciwami okręgu są równe, więc IZABC | -180° - (46°+54°)=80*

2.49    5.

Wskazówka. Ka/dy punkt należący do symetralncj odcinka jest jednakowo oddalony od końców odcinka.

2.50    3.

Wskazówka. Każdy punkt należący do dwusiecznej kąta jest równooddalony od ramion kąta.

2^1 izAS«=i4(r. \zbsc\= ioo\ izó.vn= 12(1".

rowka. S jest punktem wspólnym dwusiecznych kątów trójkąta ABC.

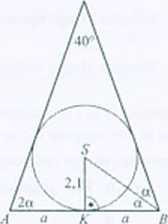
2.52 6cm.

iązanie. Trójkąt ABC jest równoramienny, więc miary kątów przy podstawie są równe. Środek Sokręgu wpisanego w trójkąt ABC leży na dwusiecznej kąta ABC.

AarW= 180°. stądrz=.35°. — = tg35°=0.7. stąd u=3. zaś Mfll=6 (cm).

c

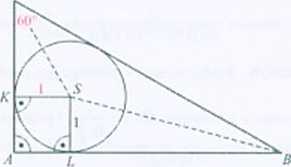
2.53 Przypmstokątnc: 1 + -Jl. 3 + ^3, przcciwprostokątna: 2 + 2^3. Rozwiązanie. Czworokąt ALSK jest kwadratem, więc IAAI 1.

Sjest punktem wspólnym dwusiecznych kątów trój kaja ABC. więc IZ Al.SI = 31)'. ^f=tg30". stąd IA'C1 = >/?. Zatem \AO = I + ^3.

=COS«r. więc 1/łCI=2( l + >/? ).    = tg<»0'^J. więc L4BI = 3 + fi.

2.54 LOiel5*. IZA1=65°, lzA/I=H5°. IZM =165°.