24 (559)

154

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

I .

6.21    a) -fj:    b)^:    d)    .1 ff; lift.

Rozwiązanie. £2 - zbiór pcrmutucji zbioru 11 -elementowego. | iii = 11!

Przyjmijmy, ze kolejne miejsca w kolejce ponumerowane są numerami od 1 do 11.

a)    Pierwszą osobą w kolejce mogła być jedna z. sześciu dziewczyn, ])ozostalc 10 osób można było ustawić na 10! sposobów.

7,idmlil-h    Ul 6 10!    6 10! b

Żalem Ul=6-I0!. «''»=_]5T=-_rn--_wrr = _TT.

b)    Dziewczynki na początkowych sześciu miejscach można było ustawić na 6! sposobów. Na pozostałych pięciu miejscach chłopcy mogli

ustawić się na 5! sposobów. Zatem |/?|=6!-5!. /'(A) **    5_ _J_

'iii II! 6I-7-8 91011    462 ’

c)    Dziewczynki musiały stanąć na miejscach \, 3.5.7,9, W. Na wymienionych sześciu miejscach mogły ustawić się na 6! sposobów. Na pozostałych pięciu miejscach chłopcy mogli ustawić się na 5! sposobów. Zatem I C[=6! • 5! PtC)- — = ^6! ^ - —L

liil II! 462'

d)    Dziewczynki musiały stanąć na miejscach I - 6 lub 2-7 lub ... lub 6 - 11 Miejsca w kolejce dla dziewczynek można więc było wybrać n.i 6 sposobów , leżeli wybrane zostały miejsca, na których miały stać dziewczynki, to można je było ustawić na wybranych miejscach na 6! sposobów. Chłopców można wtedy było ustawić na pozostałych pięciu miejscach na 5! sposobów. Zatem ll)l-6 6! 5'. P(D)~ =Ik^y^v ₌ J_.,

e)    Miejsca w kolejce dla Hani i Marcina można było wybrać na II) sposobów [miejsca I. 2 lub 2. 3 lub ...lub 10. 11). Hania mogła stać bczpo-

•srcdnio przed Marci/lCJll Jłłh Mm bezpośrednio pr/ed Hm:j. więc tę dwójkę dzieci można było ustawić na 2 ■ !() sposobów. Jeśli Hanu i Marcin stanęli na sąsiednich miejscach, to pozostałe 9 osób mo/na było ustawić na pozostałych dziewięciu miejscach na ')! sposobów. Zatem

!/:l = 2- 10-9! = 2' 10!. /»<£)= ^ =-^ ■

I) Miejsca w kolejce dla Kani i Marcina mo/na było wybrać na 5 .sposobów (miejsca 1. 7 lub 2. S lub ... bib 5. 11). Hania mogła siać bliżej początku kolejki ni/ Marcin lub Marcin mógł stać bliżej początku kolejki niż. Hania, więc tę dwójkę dzieci mo/na było ustawić na 2 • 5 sposobów. Jeśli Hania i Marcin zajęli odpowiednie miejsca, to pozostałe 9 osób można było ustawie na pozostałych dziewięciu miejscach na 9! sposobów.

Zatem |£|»2-5-9!=l0!. m')=~    = -pj--

6.22    a)    b)    C)    d)

Rozwiązanie. Przyjmujemy, ze zbiorem zdarzeń elementarnych 12 jest zbiór 5-clcmcnlowych podzbiorów zbioru ID-elcmcntowego. Liczbą

......    . |^| pOj |0!    5!-6-7-8-9-10    , „ „

wszystkich zdarzeń elementarnych: |12l = | ,. j =    = —yy-y ^ ^ — - = 47-9.

a)    A - zdarzenie polegające iui wylosowaniu pięciu kul białych. I Al = | * j =6. A4l = yy = — ^

b)    H - zdarzenie polegające na wylosowaniu dok ładnie czterech kul białych. | fil=| ^ | • |^ j = 3 • 5 • 4. Pi 0) = M = yy— = -q-.

c)    C - zdarzenie polegające na wylosowaniu co najmniej czterech kul białych. Zauważmy, że C A kj li i A r>B = 0 [patrz punkty a) i b)). Zatem /’<C) = PyA) + P[B) - ±*■“j-

d)    l>- zdarzenie polegające na wylosowaniu co najmniej jednej kuli białych.

Zdarzeniem przeciwnym do zdarzenia /> jest zdarzenie ,\ i patrz punkt a)). Zatem Pd)) I - Pd)' i 1 -P(Ą) = I = ~-

42    42

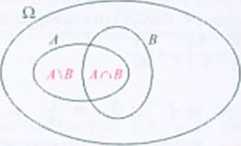
6.23 a)/'</!|=0.7;    b) mr.»)=0.2:    c) l\A\B) = 0.2.

Rozwiązanie, a) Wiemy, ze P[B)+PtB^>)= I. więc P(B)~ 1 -P[B") = 1 -0,3 =0,7.

b)    Ze wzoru P[AuB) = P[A)+ PiB)-l*[AnB) wyznaczamy

l\AnB): P(AnB)=P(A)+P(B)-P[AvB). Zatem /><An«>*0.4+0.7-0.9 =0.2.

c)    I SPOSÓB hA\B) = P(A)~ P[Ar\B) (patrz rys.). Z punktu b) mamy P(At~\B)=0.2. Zatem PiA\B) = 0.4-0.2 = 0.2.

II SPOSÓB. P(A \ B) = P[A u B) - PUD = 0.9 -0.7 = 0.2.

6.24 Wl=4. ««)b1.

•1    4

Rozwiązanie. Wiemy, scACiB 0 i AkjB-LI, więc zdarzenia A i II .są zdarzeniami przeciwnymi, a to o/nac/.a, że /VI i + PiB)~ I. Wprowadźmy oznaczenie: p-P(A>. Wówczas P(Bi= I -p. Wiemy. /e/H 1 -/») =—. Rozwiązaniami tego równania kwadratowego są liczby

/. = -!-oraz p = 4. Jcślip = 4. to P(B)= 1 -/? = 4. ajeśli/»=4* io/tfl)=4-

4-1    4    4    4    4

P[A)>P(B). więc P[Ą) = -i. zaś /'(/!)= -~.