36 (332)

166

ODPOWIEDZI, WSKAZÓWKI. ROZWIĄZANIA

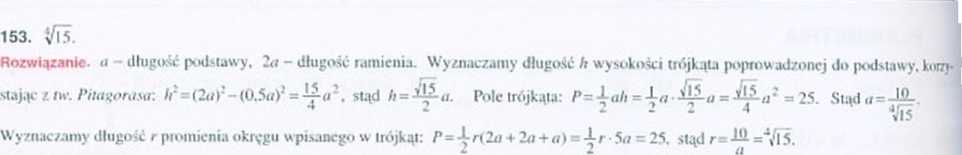
r

154. 2^5. Rozwiązanie. Punkt .S jest środkiem oktęgu opisanego na trójkącie ABC. więc odcinki SC i SB są promieniami lego okręgu. Zatem I SU! 5.v. Z n«\ Pitagorasa dla trójkąta PPS <3r)‘ ^ł 2’=(5vi^:. Stąd i =0,5. a Pr| =Ki =4. Z nv. Pitagorasa dla trójkąta PUC Ir-4* + 2‘. Stąd b= 2v'5.	7 / ^V	5t\ V^1
155. 30*. 60 . W^0.		.1. X \
156. .) ^2f. b, Rozwiązanie, h - długość wysokości poprowadzonej do podstawy.	A 2	’ 2 •

lr + 2*=X\ stąd // = 2 vl 5- Obliczamy pole trójkąta ABC:    • 4 2*15 = 4yl 5.

a)    Skorzystamy ze wzoru na pole trójkąta P -Lnr/-r/; + <-). gdzie rjesl długością promieniu okręgu wpisunego w trójkąt. Ai\5=\ń4 + 2-X). ^s,-l^l* r = -2fll.

b)    Skorzystamy ze wzoru na pole trójkąta /’    gdzie K jest długością płomienia okręgu opisanego na trójkącie.

4.^;i5=AJyŁ, stąd U =

4A    Vl5

157.

Wskazówki. I SPOSÓB. Środkowa trójkąta prostokątnego poprowadzona z wierzchołka kąta pnwego jest dwa razy krótsza ik! pr/cciuprostokątnej. II SPOSÓB. Skorzystaj z nr. >> oiUinkułąrwym środkiboków trojkąu).

158.

Ł

I0 •

Rozwiązanie, o. I< - długości pr/yprostokąlnych. c - długość przeciwprostokątnęj trójkąta prostokątnego.

Musimy obliczyć wartość iloczynu    czyli wartość wyrażenia Wiemy, Ze zachodzi równość 5-i«b = ⁱ-^-. Dzieląc obie strony

v

.    •    S

tej rownosci przez otrzymujemy

159.

:n

160. 3(2^3-3).

161. —7=-.

s/3

Jpżi

sintz

Istna 2    4

^162, \^2(sin"+l)

Rozwiązanie. P = \l>~ sin«. stąd b - \-ĄI—    & = .sin4r. zatem a = />sin-2- = J-i^-sin^-.

2    istna b 2    2 Vsin« 2

I    SPOSÓB /‘ = lr(2<f + 2fc>=r(<f+A). Zatem r =~~ - -£-=-^l--= f^/>>iDł/ -

/rsin^+b U/’(_sina _{+ n} v2(sinf+l) * istna -

II    SPOSÓB. ZABCl = ¹    Śn^,llŁ'k S okręgu wpisanego w trójkąt jest punktem przecięcia dwu

c

siecznych kątów trójkąta, więc (i~0.5-1 ZAB(.'\ = ^IS—^

— = 1 *fi. zatem r z;tg//- i'-- ' sin -^- tg-^IHf| ■ — . »    ^    Vsin a 2 ^b 4