422 (10)

422 11. Straty mocy i sprawność maszyn prądu przemiennego

rzona przy indukcji B_f i częstotliwości /; B_fc — indukcja w rdzeniu; m_F, — masa rdzenia, w kg; a — wykładnik potęgi, w przybliżeniu a = 2.

Jeżeli w porównaniu z warunkami pomiaru stratności Ap_B./ w rdzeniu występuje zarówno inna indukcja B_Ft, jak i częstotliwość f_Ft oraz nie jest znany rozdział stratności na składniki: histerezowy oraz wiroprądowy, to w przybliżeniu straty można obliczyć wg wzoru

przy czym B_p; f_r — indukcja oraz częstotliwość występujące przy pomiarze stratności Apa./-

Stratność blachy powinna być mierzona przy wartościach częstotliwości oraz indukcji zbliżonych do występujących w projektowanym rdzeniu. Wytwórcy blach magnetycznych podają stratność Ap_l/S0 lub Ap_li5/50, tj. wyznaczoną przy indukcji 1 T lub 1,5 T i częstotliwości 50 Hz

W bardziej dokładnych obliczeniach strat mocy należy uwzględnić niejednorodność pola magnetycznego w rdzeniu i oddzielnie rozpatrywać straty występujące wskutek bisterezy oraz prądów wirowych f 11.1],

W zębowych odcinkach rdzenia występuje przemagnesowywanie osiowe. Jeżeli powierzchnia przekroju zęba jest na całej wysokości taka sama oraz jeśli pominie się obciążające działanie żłobków, tzn. założy się, że indukcja w całej objętości zęba jest taka sama, to straty podstawowe można obliczać ze wzorów (11.8), przyjmując współczynnik k, w 1,5.

W zębie o powierzchni przekroju zmieniającej się wzdłuż jego wysokości (rys. 9.17) straty w zębach stojana można wyrazić wzorem

0

w którym: k_u — współczynnik wzrostu strat w zębach na skutek procesów technologicznych; 5 — gęstość blachy magnetycznej; /_F„ — długość stalowych części rdzenia wg zależności (7.46a); B^fy) — indukcja w zębie wg zależności (9.41).

Przyjmując za podstawę indukcję S*(0) w przekroju o współrzędnej y = 0 i uwzględniając, że

(11.10)

otrzymuje się

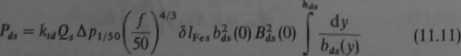
o

Ponieważ masa zębów

kś$

m_i = Q,l_f„ \ bi,(y)dy o

(H.12a)

to wzór na straty mocy w zębach można zapisać w postaci Pdt⁼    Rh (0)^mikt4

przy czym współczynnik

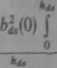
dy

bufy)

i bjy)dy o

W przypadku zęba o zarysie trapezowym współczynnik uwzględniający nierównomierny rozkład indukcji wyraża się wzorem

k* = 2

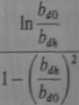
(11.13)

w którym: b_d0, b_ih — szerokości zęba, jak na rys. 9.17a.

Na podstawie zależności (l!.12b) można ułożyć program numerycznego obliczania współczynnika k_u dla dowolnego kształtu zęba. W celu uwzględnienia odciążającego działania żłobków na strumień w zębach oraz na występujące w nich straty mocy, indukcję wzdłuż wysokości zęba wyznacza się w sposób podany na rys. 9.18. Wartość współczynnika ku zależy od dokładności wykonania, stopnia zużycia oraz od obsługi wykrojników, a także od sposobu izolowania wykrojów oraz ciśnienia wytwarzanego w spakietowa-nym rdzeniu i zawiera się w przedziale l,4-r2£

Straty mocy w jarzmie oblicza się przyjmując założenia upraszczające co do rozkładu pola magnetycznego oraz charakteru przemagnesowy-wania. W obliczeniach przybliżonych przyjmuje się, że amplituda indukcji jest w każdym punkcie jarzma taka sama i równa indukcji maksymalnej wynikającej z zależności (9.53). Ponadto zakłada się, że przemagnesowanie jest osiowe. W obliczeniach bardziej dokładnych uwzględnia się w przybliżony sposób nierównomierny rozkład indukcji oraz występowanie przemagneso-wywania obrotowego o niejednakowym współczynniku eiipiycznośd pola magnetycznego [3].

Obliczenie strat mocy w jarzmie na podstawie przesłanek teoretycznych jest jednak bardzo pracochłonne, a ze względu na trudny do przewidzenia wpływ czynników technologicznych — nie zapewnia osiągnięcia wyników zgodnych z pomiarami.