542 [1024x768]

552

KOLOIDY

gdzie: r — promień kapilary: /—długość kapilary; x— odległość warstwy cieczy od ścianki, ą — lepkość cieczy.

Jeżeli d oznacza grubość warstwy podwójnej, to x =» r-d, a ponieważ d    r, zatem

r² — x² — r² — (r—d)² = 2 rd+d² = Ird

Wstawiając tę wartość do równania (7.67) otrzymujemy:

prd

W

(7.68)

Ruch ładunków w warstwie podwójnej względem siebie jest równoważny przepływowi prądu elektrycznego, którego natężenie otrzymamy mnożąc wielkość powierzchni warstwy podwójnej przechodzącej przez przekrój poprzeczny kapilary w ciągu I sek (czyli 2nrv) przez powierzchniową gęstość ładunku w warstwie podwójnej o:

I = 2txrvo

(7.69)

Wstawiając do tego równania prędkość przepływu cieczy przez kapilarę. wyrażoną za pomocą wzoru (7.68) otrzymamy:

(7.70)

Przepływowi prądu towarzyszy opór elektryczny /?, którego wielkość określa U prawo Ohma:

R

i

w którym * oznacza przewodnictwo właściwe cieczy. Potencjał przepływu E_p otrzymamy mnożąc wielkość prądu przez opór:

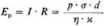
zaś po podstawieniu wartości powierzchniowej gęstości ładunku o, z równania na potencjał elektrokinetyczny £ (7.61), otrzymujemy:

Równanie to może być wykorzystane do wyznaczenia potencjału C przez pomiar ciśnienia hydrostatycznego p dla danego E_p. Jednakże kapilary nie mogą być zbyt wąskie, gdyż w tym przypadku przewodnictwo w kapilarach może różnić się od wartości x w głębi roztworu.