531 [1024x768]

542

KOLOIDY

gdzie

32?t³ • rt₀ 32⁴ • N_a

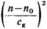
H =

W roztworach rozcieńczonych wyrażenie | —J przedstawiające przyrost

współczynnika załamania światła na jednostkę stężenia gramowego, może być zastąpione przez pochodną d/i/dc_t, stąd:

32r^s • n₀

n_a

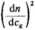
(7.60)

Mierząc zatem współczynnik załamania ośrodka rozpraszającego dla danej długości fali świetlnej n₀ oraz wyznaczając órtfóc_g dla roztworu koloidalnego, można wyznaczyć H (z równania 7.60), zaś poprzez pomiar współczynnika zmętnienia możemy obliczyć (z równania 7.59) masę cząsteczkową A1.

Bardzo interesujący jest przypadek, w którym cząstka koloidalna ma wymiary współmierne z długością fali światła stosowanego do badania rozproszenia. W tym przypadku rozproszenia, z różnych miejsc cząstki będą ze sobą interferować i będziemy mogli obserwować asymetryczny rozkład natężeń światła rozproszonego. Zjawisko to jest podobne do rozpraszania elektronów na różnych atomach tej samej cząsteczki, co jest przedmiotem badań elektro-nografii. Potrzebne informacje otrzymuje się przez pomiar natężenia światła rozproszonego pod kątami 45° i 135° w stosunku do kierunku wiązki padającej.

°0    0,2 04 0^6 <X8 \,0

xl).

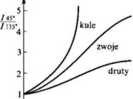
Rys. 7.10. Zależność natężenia światła rozproszonego    jj*) od parametru długości

cząstek koloidalnych dla różnych typów cząstek

Odkładając zależność /45//135 jako funkcję xJX, otrzymuje się charakterystyczne krzywe w zależności od kształtu cząstki (rys. 7.10); x oznacza tu wymiar liniowy cząstki koloidalnej (np. średnicę w przypadku cząstek kulistych lub długość w przypadku cząstek „drutowych” itp.), zaś /. jest długością fali stosowanego do badań światła.