8 (1445)

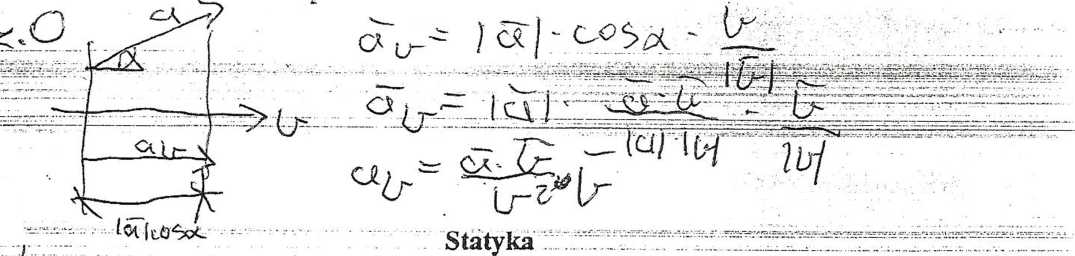
-l.Siła: Siły-zdefiniować -nie możemy, ale możemy ją zmierzyć poprzez pomiar skutków jej działania------------------------------

(nadanie ciału przyspieszenia, lub w przypadku ciał odksztalcalnych—jego deformację). Dla celów praktycznych „definiujemy³’ siłę jako oddziaływanie jednegociałanadrugie; Oddziaływanie' takie może być realizowane na drodze bezpośredniego kontaktu tych ciał, lub na odległość (siły grawitacji, magnetyczne, elektrostatyczne itp.).

C2. Zasada 1    ...................

Dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy, gdy działają wzdłuż jednej prostej, są przeciwnie skierowane i mają te same wartości liczbowe.

Zasada 2

Działanie układu sił przyłożonych do ciała sztywnego nie ulegnie zmianie, gdy do tego układu zostanie dodany lub odjęty dowolny układ równoważących się sił (tzw. TJłdad zerowy). Interpretacja pierwszej zasady statyki

Interpretacja drugiej zasady statyki Do ciała sztywnego zawsze można przyłożyć dwie równe co do wartości .......—

liczbowej i przeciwnie skierowane siły, działające wzdłuż tego samego kierunku. Zerowe układy sił wykorzystywane

są dc identyfikacji sił działających na elementy konstrukcyjne,--------- ------------- -----------------,-----------

Z zasady 2 wypływa ważny praktyczny wniosek, że każdą silę działającą na ciało sztywne można dowolnie przesuwać wzdłuż kierunku jej działania. Wektor, który może być dowolnie przesuwany wzdłuż kierunku działania, nazywa się wektorem przesuwnym. Siła działająca na ciało sztywne jest wektorem swobodnym.

Zasada 3

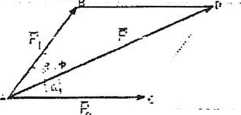
Dowolne dwie siły PI i P2 , przyłożone do jednego punktu,

można zastąpić siłą wypadkową R przyłożoną do tego punktu i przedstawionąjako wektor będący przekątną równoległoboku ABCD zbudowanego na wektorach sił w sposób pokazany na rysunku.

Zasada 4

Każdemu działaniu towarzyszy równe co do wartości i przeciwnie skierowane wzdłuż tej samej prostej przeciwdziałan ie.

Zasada 5

Każde ciało nieswobodne można myślowo oswobodzić od więzów, zastępując przy tym ich działanie odpowiednimi reakcjami. Dalej ciało to można rozpatrywać jako ciało swobodne, podlegające działaniu sił czynnych (obciążeń) oraz sił biernych (reakcji).

3.

2 2 2

a=\ ax + ay + az -długość wektora ax=yafcosa

ay=ąi*cos',^długości rzutów na osie układu współrzędnych. az=ą;*cos \ v

4.

Przekształcenie elementarne a - usunięcie lub dołączenie do układu sił A układu złożonego z dwu wektorów przeciwnych ieżących na jednej prostej tzn. układu sił.

Przekształcenie elementarne j3 lub dołączenie do układu sił A układu złożonego z kilku wektorów o wspólnym punkcie zaczepienia i o sumie równej wektorowi zerowemu tzn. układu sił.

Wykonując na układzie sił przekształcenie elementarne nie zmieniamy jego działania statycznego i dynamicznego. W układzie sił wolno przesuwać siłę wzdłuż jej prostej działania.