CCF20090319044

Zasady całkowania 53

Ten ostatni zapis wyraża oczywisty fakt, że w wyniku różniczkowania, a następnie całkowania funkcji F(x) otrzymujemy tę samą funkcję z dokładnością do stałej C. Widzimy również, że

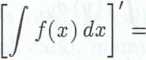
/(aO-

Wyznaczanie całki nazywamy całkowaniem funkcji. Całkowanie, w przeciwieństwie do różniczkowania, nie jest działaniem jednoznacznym. W wyniku całkowania funkcji otrzymujemy nieskończenie wiele funkcji różniących się o stałą C, zwaną stałą całkowania.

Zgodnie z definicją (3.1) mamy:

J 1 dx = J dx = x + C;

z : mieść liczbę do-"i 15: ek kwadratowy, bia początkowego.

ozsrotnymi. Przy-euc renie i dzielenie, ■oególności działa-11 uny na przykład

= const.

aie a.b) nazywamy : . ;:ałą. i oznaczamy

i

(3.1)

31 całkowania, /(x) dx funkcji f(x). u ą zawsze razem, jak zz ;:ając z oznacze-

= F{z) -(- C.

/

x^kdx

x^k+1 k + 1

+ C, gdzie x ^ 0, k ^ —1;

r dx

J X

ln |z| + C;

a^xdx = ---I-C, a > 0, a ± 1;

ln a

J cos x dx = sin x + C, j sii

/ —dx = tg x + C, I —%— dx = -ctgz + C. J cos^ x    J sm x

sin x dx — — cos x + C;

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

Podane, wzory łatwo sprawdzić przez zróżniczkowanie prawych stron równań. Czasem, aby uprościć zapis, opuszcza się stałą całkowania.

3.2. Zasady całkowania

Stałą A można wyłączyć przed znak całki, tzn.

J Af(x)dx = A J f{x)dx.

Całka sumy (różnicy) jest równa sumie (różnicy) całek, czyli

(3.7)

J [f{x)±g(x)] dx =

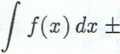
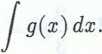
(3.8)