CCF20090319055

64

Całkowanie

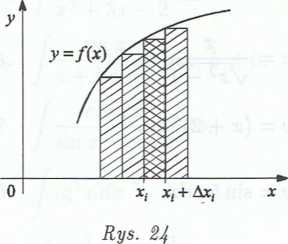
Historycznie, symbol J , będący zmodyfikowaną literą 5, oznaczał sumowanie nieskończenie wielu składników postaci y{Ax{, zwanych elementami pola (zob. rys. 24).

Całka oznaczona jest granicą sum o rosnącej liczbie składników, tzn.

Inne własności całki < wzory (3.7) - (3.12).

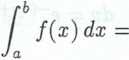
lim V yiAx{.

n—

Przykłady

1. Obliczyć całkę ona

i=1

Rozwiązanie. Licz** nice całkowania. kCa (x + l)². Po zasi

Tak więc

/

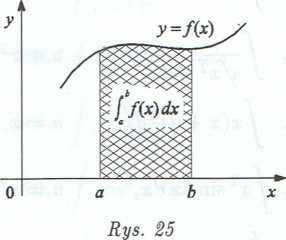
Jeśli więc w przedziale (a, b) funkcja /(x) jest nieujemna, to całka oznaczona

rb

_ ' - J

r- —

/ /(*)

J a

dx

jest równa polu obszaru ograniczonego łukiem krzywej y = /($), osią Ox oraz prostymi x = a i x = b, jak widać na rysunku 25. Jeżeli zaś w przedziale (a, b) funkcja f(x) jest ujemna, to analogiczne pole jest równe

- f f(x)dx.

J a

Zawsze więc pole określonego wyżej obszaru można wyrazić całką oznaczoną

/ \f{x)\dx.

J a

Łatwo sprawdzić, że dla całki oznaczonej prawdziwe są następujące wzory:

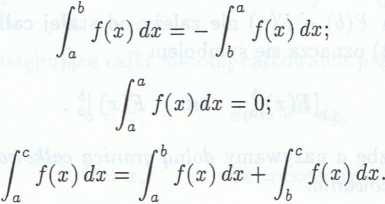
2. Obliczyć pofe oka V = x²-

Rozwiązanie. SzAi przecięcia r:: -' -ustalić granice ca£EW wiązaniu układa ión

y = z².

2x-f-3

otrzymujemy xi = —1 kane pole 5 jes: cinkiem AB minns ] mentem parabol (ad

5 = £ :

=