CCF20110506015

(7—99)

U_w. = u₁

można zamiast równania (7—97) napisać równanie uproszczone:

U^L,^    (7-100)

Napięcie U_v panujące na uzwojeniu z_p jest transformowane do uzwojeń z₂ i z_b. Napięcie indukowane w uzwojeniu z_b ma wartość:

(7-101)

Zi

Dzięki zgodnemu kierunkowi nawinięcia uzwojeń z₁ i z_b napięcie podawane na bazę tranzystora jest dodatnie w stosunku do emitera. Powoduje to przepływ prądu bazy I_B o wartości:

1

B~

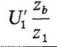
RB + ^rb

(7—102)

gdzie:

R_b — rezystancja zewnętrzna w obwodzie bazy, r_b — rezystancja wejściowa tranzystora równa U_BE/I_B.

W uzwojeniu z₂ indukuje się napięcie o wartości:

ŁS=ię-    (7-103)

^Z1

Dzięki odwrotnemu kierunkowi nawinięcia uzwojeń z, i z, napięcie podawane na anodę diody D jest ujemne. Dioda jest więc spolaryzowana wstecznie. W czasie przewodzenia tranzystora dioda D nie przewodzi, w uzwojeniu z₂ nie płynie więc prąd. Prąd kolektora tranzystora T narasta liniowo zgodnie z wzorem:

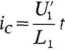
(7—104)

aż do uzyskania wartości równej:

^Cmax—^FE^B    (7    105)

gdzie I_B ma wartość określoną wzorem (7—102).

Przy danym prądzie bazy maksymalny prąd kolektora zależy tylko od wzmocnienia tranzystora. W czasie narastania prądu kolektora tranzystora wzrasta też strumień w rdzeniu transformatora, aż do uzyskania wartości <D_m. Czas narastania prądu i_c i strumienia O (czas t. na rys. 7.24) można określić podstawiając I_c max zamiast i_c do wzoru (7—104). Czas ten wyraża się wzorem:

t,=

LJ_C

u;

(7—106)

Między napięciem U[ a zmianą strumienia w rdzeniu transformatora zachodzi zależność:

d&

u;=_Zl—    (7-107)

Zmiana strumienia w czasie t_z równa jest <P_m, a odpowiadająca mu zmiana indukcji równa jest B_m. Uwzględniając zależność: -

<P = S_FeB    (7—108)

gdzie S_Fe jest powierzchnią przekroju rdzenia transformatora, wzór (7—107) możemy zastąpić wzorem:

u;=

U ^Fe^m

(7—109)

Gdy prąd kolektora tranzystora osiągnie wartość I_c max, przyrost prądu d;_c/'d/ staje się równy zeru. Następnie prąd kolektora zaczyna się zmniejszać. Zmniejsza się również napięcie indukowane w uzwojeniu z_b i prąd bazy I_B, co powoduje dalsze zmniejszanie się prądu kolektora. Wystąpienie w tym momencie dodatniego sprzężenia zwrotnego powoduje bardzo szybkie zmniejszenie prądu i_c do zera.

W momencie zaniku prądu kolektora tranzystora strumień w rdzeniu nie może zmienić się raptownie. Zmienia się tylko kierunek jego zmian. Od tej chwili zaczyna się on zmniejszać. Zmiana kierunku zmian strumienia w rdzeniu transformatora powoduje zmianę kierunku napięć indukowanych w uzwojeniach. Dioda D zostaje spolaryzowana w kierunku przewodzenia i zaczyna przewodzić. W momencie gdy dioda D zaczyna przewodzić, płynący przez nią prąd z₂, równy prądowi uzwojenia z₂, ma wartość:

*2(0)^— Ic

Łl

z₂

(7—110)

Dzięki przepływowi tego prądu energia zmagazynowana w indukcyjności głównej transformatora rozładowuje się poprzez diodę D zasilając odbiornik i ładując kondensator C. Energia ta w momencie rozpoczęcia rozładowania ma wartość:

W=\ LJl max    (7-11D

Między napięciem na uzwojeniu z₂ a zmianą prądu i₂ zachodzi zależność:

U₂ =

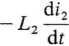
(7—112)

gdzie L₂ jest indukcyjnością główną transformatora widzianą od strony zacisków uzwojenia z₂.

Między indukcyjnościami Lj i L₂ zachodzi zależność:

17* 259