CCF20140115003

36 Henryk Moroz

36 Henryk Moroz

r + r + r + r    +    r    =    p,

5    •    r    =    p,

p    :    5    =    r,

1

T    •    P    =    ^r>

2 + 2 + 2+ 2 + 2 = 10,

5 • 2 = 10,

10 : 5 = 2,

1

— • 10 = 2.

Wymienione tutaj działania arytmetyczne są wprowadzane słownie, bez symboli, jeszcze przed poznaniem cyfr.

Umiejętność rozkładu Jiczb-fia składniki opanowują uczniowie w trakcie zabawy w kolorowe dywany. Wybierają najpierw dowolny klocek, a następnie układają pS5l?nef"§amej długości z dwóch lub większej Rys. 4 liczby klocków (rys. 4).

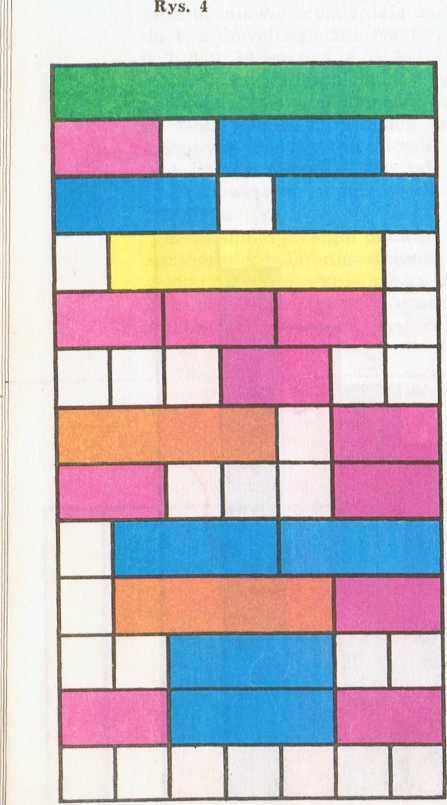
7

2+1+3+1

3 + 1+3 1 + 5 + 1

1+1+1+2+1+1

4 + 1 + 2

2+1+1+1+2 1 + 3 + 3 1+4 + 2 1 +1 + 3+1 + 1

2 + 3 + 2

t

1+1+1+1+1+1+1

W trzecim etapie w,pmwadza się pisane symbole matematyczne: cy-fry 0^1,2,. „3,.A, 5,~6,-7_y-8,9_r-znaki "działań arytmetycznych: +, —,    :

oraz symbol rów.nościi =,JUmniejszości <C Przydatność liczb w kolorach w praktyce szkolnej najtrafniej określa prof. dr A. Z. Krygowska: Już na wstępie więc organizuje się czynności dziecka z punktu widzenia całej struktury arytmetyki liczb naturalnych; pojęcie liczby formuje się od początku w ścisłym związku z działaniami arytmetycznymi; a więc nie najpierw liczba, a potem działanie, ale z systemu działań algebraicznych, z ich własności wyłania się pojęcie liczby. Znaczenie tego pojęcia dla rozwoju myśli matematycznej Ucznia rozumie dobrze ten nauczyciel, który nie może wytępić błędów w rozwiązywaniu równań typu: a — x = b, x — b — a lub a ‘ x — b, x = b — a, gdyż uczniowie nie widzą związków między działaniami, przyswajano im bowiem mechaniczne nawyki, które często zawodzą, a nie zrozumienie struktury algebraicznej ([M. 18], str. 95).

7.4.    kl asności dodawania i odejmowania

7.4.1. Zakres materiału programowego

Zgodnie z wymogami programu z 1978 r. dzieci zapoznają się z podstawowymi własnościami dodawania i odejmowania od klasy pierwszej. Znajduje to m.in. wyraz w takich hasłach programu jak: „Praktyczne przedstawianie przemienności dodawania. Zadania typu: 4 + 0 = 4, 5 — 5 = 0, 5 — 0 = 5, (...). Wprowadzenie nawiasu, np. 7 + 5 = = (7 + 3) + 2 = 10 + 2”. Hasła te odczytamy jako polecenie pro-pedeutycznego przerobienia przemienności i łączności dodawania oraz roli zera w dodawaniu. Natomiast w programie klasy II hasła „prze-mienność dodawania” i „łączność dodawania” sformułowane są wyraźnie.

Oczywiście odejmowanie nie jest przemienne, ani łączne. Zwrócenie jednak uwagi dzieciom na ten fakt jest bardzo pożądane, bowiem przekazywanie im w sposób naturalny intuicyjnego sensu przemienności dodawania mogłoby sugerować błędnie, że odejmowanie ma też tę własność.

7.4.2. Przemienność dodawania

Prawo przemienności dodawania mówi, że dodawanie liczb możemy wykonywać w dowolnej kolejności, wynik dodawania nie Zależy od kolejności składników albo jeszcze inaczej — wartość sumy nie zależy od kolejności dodawanych składników. Każde z tych sformułowań słownych zastąpić można krótkim zapisem literowym:

a + b = b + a,

przy czym rozumiemy to w ten sposób, że powyższa równość zacho-