CCF20130109030

5> = 0; V_A+V_B+V_c-q-2l + P-q-3l = 0,

^M_a=0;    P-2l-q-2l-l-M-V_B-2ł + q-3l-2,5l-V_c-4l = 0,

Yj^Me= 0; P-3l + V_Al-M-q-2l-2l = 0 stąd otrzymujemy:

H_a=0,    V_a=2 ql,    V_B=jql, V_c=^ql.

Przedziałami belki są odcinki DA , AE , EB , BC .

Współrzędne przekrojów, w których będziemy określać funkcje T(x) i Mg(x) obieramy zgodnie z rysunkiem 3.19. Funkcje sił poprzecznych i momentów zginających oraz ich wartości dla granic przedziałów zmienności zestawiono w tablicy 5.

Tablica 5

Granice przedziału	T(x)	Mg(x)	Wartości
			X	m	Mg{x)
(N VI *" VI	P~qx i	^Px\ -q X] ~	0	qi	0
			21	-ql	0
21 śx2ś 31	P-2ql + VA	P-x2-lql■ {x2 -/)+ VA ■ (x2 - 2l)-M	21	qi	-qP
			31	qi	0
0Sr,<2 /	~Vc+qx 3	Vc-x<-qx2-h-	0		0
			21	7*^1
2 lśx4ś 31	-K+qx4-vB	^vc-x4-q-xA ~ + VB-(x4-21)	21	0	b^1’
			31	qi	0

Jak wynika z otrzymanych w tablicy 5 wartości, siła poprzeczna zmienia znak w przedziale DA (xi e < 0; 21) i CB (x₃ e < 0; 21).

/ równania T{x_w) = U otrzymujemy współrzędną, dla Której sita poprzeczna n iw ii.i jest zeru, a mianowicie:

(/I — q ■    — 0, stąd — 1.

Moment ekstremalny M_maX| wynosi: l    1    2

AC*, =^M\ *,„=/ = ^ql ■

Anillogicznie z równania T(x₃ą) = 0 mamy:

)ql + q-x₃₀ = 0, stąd x₃₀=^-l.

4    4

Nli iment ekstremalny A/_maX2 jest równy:

^max, ^

_25 _/2

5 — V

*» 4'    32

4

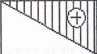
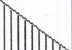
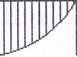
na rysunku 3.20.

Wykresy sił przekrojowych przedstawiono

M=qf

nr~	l 1 V	11 i	i i i t
; P=ql			\	[^vc

ł ' ł ' ł

BTlUw

©

w¹

^■pr ■^qjąi

i _i2

w

Rys. 3.20

57