DSC00135 (2)

1

Egzamin z ekonomii matematycznej

Nazwisko i    .......dat».?;;^- - ŁoqJ

Odpowiedz, czy podane niżej zdania są fałszywe, czy prawdziwe (P luk F)

1. Ekonomia matematyczna obejmuje zastosowania matematyki do rozumowania dedukcyjnego (P

2. Równanie S = 1 jest typem równania behawioralnego

i

3.    Liczby y2 i 27³ są liczbami niewymiernymi. P

4.    Jeśli w liniowym modelu rynku a <c, tzn. że mamy do czynienia z rynkiem dobra, którego produkcja nie zostanie podjęta P

5. Nachylenie krzywej mierzy stopień kątowy p Wybierz prawidłową odpowiedź, wiedząc, że prawidłowych odpowiedzi może byt więcej, niż jedna:

6. Liczbą rzeczywistą j est (^) Liczba naturalna b) Rozwiązanie równania x² = — 1

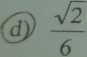
© V2

7. Funkcja jest

(a) Zbiorem par uporządkowanych ^ b) Iloczynem kartezjańskim (c) Zbiorem punktów ^

02-lut-Q9 11:40