DSC00307 (14)

Rozwiązanie

Punkt M jest w ruchu złożonym. Ruch unoszenia jest obrotowy, wokół przekątnej sześcianu, jednostajnie przyspieszony. Ruch względny jest jednostajny po 1 okręgu. Początek układu odniesienia należy przyjąć na osi obrotu sześcianu.

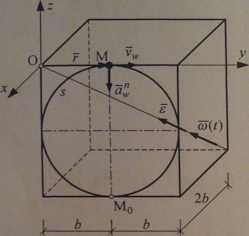
Obliczenia wstępne:

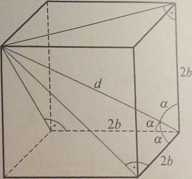
d =    (2bf + (2bf + (2bf = 2^3b (długość przekątnej sześcianu)

Ib 2b    1    t/3

COS a = - = -4- % r—

^d    2y/3 b    y/3    ³

o) i u) cos a 'e, - <o cos a -e„ + a> cos a *e = —e_T ^{x y} &

e = e cos a *e„	- - e - e cos a *e„ + e cos a *e —
r = bey
Ruch względny:
_
^vw I ^vi» ^vw	- ^v.^s,
r	W
«(0 | fvwdt +	s(0) i y^l + 0 = itb i
0	lo i 2 „2
Sg1H § o,	n ^Vw | I
jjj w *	11 b i b^y °^w i S b

fi

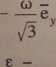
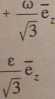
h

nb

fi