DSC07079 (6)

90

uągrosc funkcji

g)3*+x=r3, (0.1);    h)lnx + 2x=l,

|)x'“ + *- t = 0, |||| J)x2* = t, (0,1).

Wyznaczyć rozwiązanie równania g) z dokładnością 0.125.

• Zadanie 3.8

Korzystając z twierdzenia Darboux o przyjmowaniu wartości pośrednich uzasadnić następujące stwierdzenia:

a)    na każdym szlaku turystycznym wiodącym z Karpacza (800 m nad poziomem mona) na Śnieżkę (1602 m nad poziomem morza) jest miejsce, które wznosi się 1000 m nad poziomem morza;

b)    w każdym wielokącie wypukłym istnieje sieczna, która jednocześnie połowi obwód i póle tego wielokąta;

c)    na dowolnej figurze wypukłej na płaszczyźnie można opisać kwadrat;

d)    jeżeli samochód wyruszył z Wrocławia o godz. 8:00 i jadąc ze zmienną szybkością dotarł do Warszawy o godz. 12:00, a następnego dnia o godzinie 8:00 wyruszył z powrotem i jadąc po tej samej drodze wrócił do Wrocławia o godz. 1230. to jest takie miejsce na tej drodze, w którym był o tej samej godzinie zarówno jadąc do Warszawy jak i wracając z powrotem;

e)    jeżeli zegar o północy spóźniał się o 5 min, a po nakręceniu, ale bez przestawiania wskazówek, następnego dnia o północy spieszył się o 10 min, to w pewnej drwili wskazywał właściwy czas;

f*) na Ziemi są dwa miejsca, położone symetrycznie względem jej środka, w których panuje ta sama temperatura;

g*) dowolny wielokąt wypukły można podzielić dwiema prostopadłymi do siebie prostymi na cztery części o jednakowych polach.

4

Pochodne funkcji

Przykłady Podstawowe pojęcia • Przykład 4.1

Korzystając z definicji zbadać, czy istnieją pochodne podanych funkęji w zo

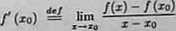
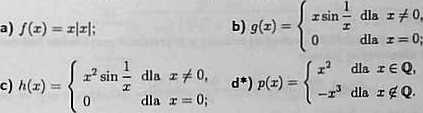
Rozwiązanie

Pochodna funkcji / w punkcie zo jest określona wzorem

lim |x| = 0. *—*o

a) Mamy

b) Mamy

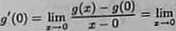
xsin--0

..    s§5— = Urn:

z —0