DSC07094 (6)

118

Pochodne funkcji

genych punktach:

a) t*(x) = 2x — |x|, xo = °:

f z² dla z< “^<x),= jy dla z>

==0 = 2;

s» /W = |*-1|. *o = l:

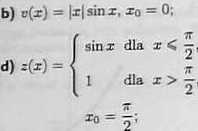
g) M*)

_ f ararctgi dla zj^O,

{

0

xo = 0;

ł*+M

dla z = 0,

dla z =£ —1,

i)?(x)={ Inlz+l|

0    dla ar= — 1,

Zn = -1;

f) g(x) = \x- flj³ sin z, z₀ =

f z² dla z < 1, ^{h)p{l) =} (v5dU_I>i,

xo = X;

zo =Ó:

dla z € Q, dla z£Q,

• Zadanie 4.2

Korzystają z definicji obliczyć pochodne podanych funkcji:

^a) «(*) = jTj. gdzie z # -1;

b) t/(z) = y/x, gdzie z > 0; c) co(z) = tg z. gdzie z^^ + fcrdlafc€Z; d) z(z) = sh z, gdzie z 6 R;

0 sto = lig, gdzie z 0; h) p(z) = sin —, gdzie x =£ 0;

BI

e) /(z) = z² — 3z, gdzie z € R; g) fc(z) = 4^X, gdzie z € 3:

0 «Kx) =ctgz_f gdzie z kx dla fc € Z;    j) r(z) = -j-j-y, gdzie z € R.

• Zadanie 43

Napisać równania stycznych do wykresów podanych funkcji we wskazanych punktach:    '\,f    ^

a)/(z) =arc«in|. (l,/(l)};    |/(*) = ln(** _+e), (0_r/(0));

c) /W(1-/(1).);    «*) /(*) = '/2*TT, (3,my,

^e>/W = T^' (^-/H)^: 0/(x) = «rctg*», (0,/CO));

|^/W | || ⁽‘-/W);    | /(*) | A (X,/(!)};

Zadania

119

• Zadanie 4.4

a) Obliczyć kąty, pod jakimi przecinają się wykresy podanych funkcji;

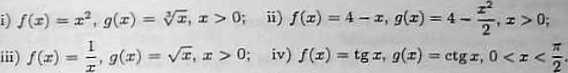
b) Dla jakich wartości parametru a € R, wykresy funkcji y = e°*. y = e“^ł przetną się pod kątem prostym?

• Zadanie 4.5

a)    Na wykresie funkcji y = e¹ znaleźć punkt, który jest położony najbliżej prostej y = ex — 4;

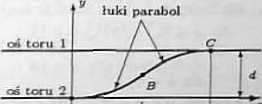
b)    Tory kolejowe biegnące równolegle trzeba połączyć rozjazdem składającym się z dwóch łuków parabol (rysunek). Odległość między osiami torów wynosi d = 8m, a rozjazd ma mieć długość / = 40 m. Należy go zaprojektować w ten sposób, aby ruch pociągów przebiegał w sposób gładki, tzn. aby w punktach A, B, C istniały styczne do osi rozjazdu. Podać równania łuków parabol w układzie współrzędnych z rysunku;

M

A

1

Zadanie 4.6

a)    Basen ma kształt odwróconego ostrosłupa ściętego prawidłowego. Dno basenu jest kwadratem o boku 4 m. a jego górna powierzchnia kwadratem o boku 16 m. Głębokość basenu wynosi 2 m. Do basenu wlewa się woda z prędkością lm³/min. Z jaką prędkością będzie się podnosił poziom wody w basenie w chwili, gdy będzie on napełniony do połowy głębokości?

b)    Gumowy balon ma kształt kuli o objętości Vq = 40 m³. Do balonu wtłacza się powietrze z szybkością p = 1 m³/s. Obliczyć, z jaką szybkością powiększać się będzie średnica balonu po 24 s. Założyć, że ciśnienie powietrza w balonie jest stałe;

c)    Drabina składa się z dwóch ramion o długości l = 2.5 m. Podstawy ramion są przysuwane do siebie z prędkością v = 5cm/s. Obliczyć, z jaką prędkością będzie podnosił się wierzchołek drabiny w chwili, gdy podstawy ramion będą oddalone orf = 3m.