DSC07096 (6)

122

Pochodne funkcji

e) Przekątna sześcianu zmierzona z dokładnością 1 mm wynosi 14.3 cm. Z jaką w przybliżeniu dokładnością można obliczyć pole powierzchni całkowitej tego sześcianu?

0 W biegu na 100 m czas mierzy się z dokładnością 0.01 s. Z jaką w przybliżeniu dokładnością można obliczyć średnią szybkość zawodniczki, jeśli uzyskała ona czas 12.50 s?

• Zadanie 4.15

Korzystając z twierdzenia o pochodnej funkcji odwrotnej oraz z różniczki funkcji znaleźć przybliżone rozwiązania podanych równań:

aj 3?⁰¹-3-2003* =2005; b) 3* -    = 8.70;

c) sinx + arctgi = 0.008; d) z + In* = 3.71; e) tf?+7 + * = Z83;    g)3* + 4*=7.1.

• Zadanie 4.16

Obliczyć /", J^m podanych funkcji: a) /(*) = z³ -    b) /(z) = zsinz;

d) /(z) = arctgz; f) /(*) = sin³ z *ł* cos³ z; h) /(z) = ch³ z + sh 2z.

c)/(z) = ę.

e)/(*) = 4z⁷-5z³+2z; g) /(*) = ** z;

• Zadanie 4.17

Zbadać, czy istnieje /*ⁿ⁾ (xo) dla podanych funkii i punktów:

a)/(x)=z^5(z|f *>-0, n = 3;	; •>)/(*)-.	U"-^15’	dla dla
		Zo = 0, n =s	2;
/ -z^3 dla z< 0, dla z>0f	«*)/(*)»!	r URI i 1 * arctg — lo	dla dla

z < 0, * > 0,

**0. z = 0,

zq s 0, n = 2;    z© == 0, n — 3.

• Zadanie 4.16

Funkcja / ma pochodne do drugiego rzędu włącznie. Obliczyć j/,y” podanych ńmkcji złożonych:

ajg-e^;    b)y*/(tgx);    c)p-x/(3x);

<*>»«/(/(**))•. «)lł = /(V^lS);    0lf = /(3*);

f) V - /(*n*)-,    h)0 = /{“«***)-

Zadania

123

•    Zadanie 4.19

Znaleźć wzory ogólne na pochodną n-tcgo rządu podanych funkcji:

a) u(z) m    b) o(x) = sin² x\ c)u<x)=¹e¹; d) z(x) = ln(l +2x);

e) ■/(¹) ¹= cos    0 9{x) = 2“¹;    g) h(x) = 11 H¹) fc(x) = e¹aln5x.

•    Zadanie 4.20

a)    Punkt materialny porusza się po krzywej y = V w ten sposób, że jego rzut na oś Oz ma stałą prędkość v_x = 3. Z jaką prędkością (w kierunku osi Oy) porusza sie ten punkt w chwili, gdy jest na wysokości 4?

b)    Punkt materialny porusza się ze zmienną szybkością wzdłuż osi Oz. Położenie tego punktu w chwili t jest opisane wzorem

x(t) = 3 • 2¹-ł-2^r3‘.

Obliczyć przyśpieszenie punktu w chwili, w której jego szybkość jest równa 0.

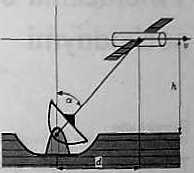
c)    Stacja orbitalna porusza się prosto-liniowo na wysokości h = 400 km nad Ziemią z szybkością v = 500 km/godz. Antena odbierająca sygnały znajduje się bezpośrednio pod trajektorią stacji (rysunek). W każdej chwili oś anteny jest skierowana na stację. Obliczyć szybkość kątową anteny w chwili, gdy stacja znajdzie się w odległości d = 200 km ód anteny.

1

   Zadanie 4.21

a)    Złożona drabina strażacka ma długość 10 m i jest pozioma. Przy rozkładaniu drabiny podnosi się ona z prędkością kątową u = — rad/min i jednocześnie wysuwa z prędkością w = 5 m/min. Z jaką prędkością będzie się poruszał strażak w koszu na końcu drabiny po 3 minutach wznoszenia?

b)    Położenie cząstki w chwili t opisuje wektor wodzący ?'= (e^łcost,e^frin<,c¹). Znaleźć przyspieszenie cząstki w chwili, gdy wektor prędkości miał długość \/3;

c)    Wskazówka minutowa zegara na ratuszu ma długość 3 m, a godzinowa 2 m. Obliczyć prędkość, z jaką oddalają się od siebie końce wskazówek zegara o godzinie 6:00.